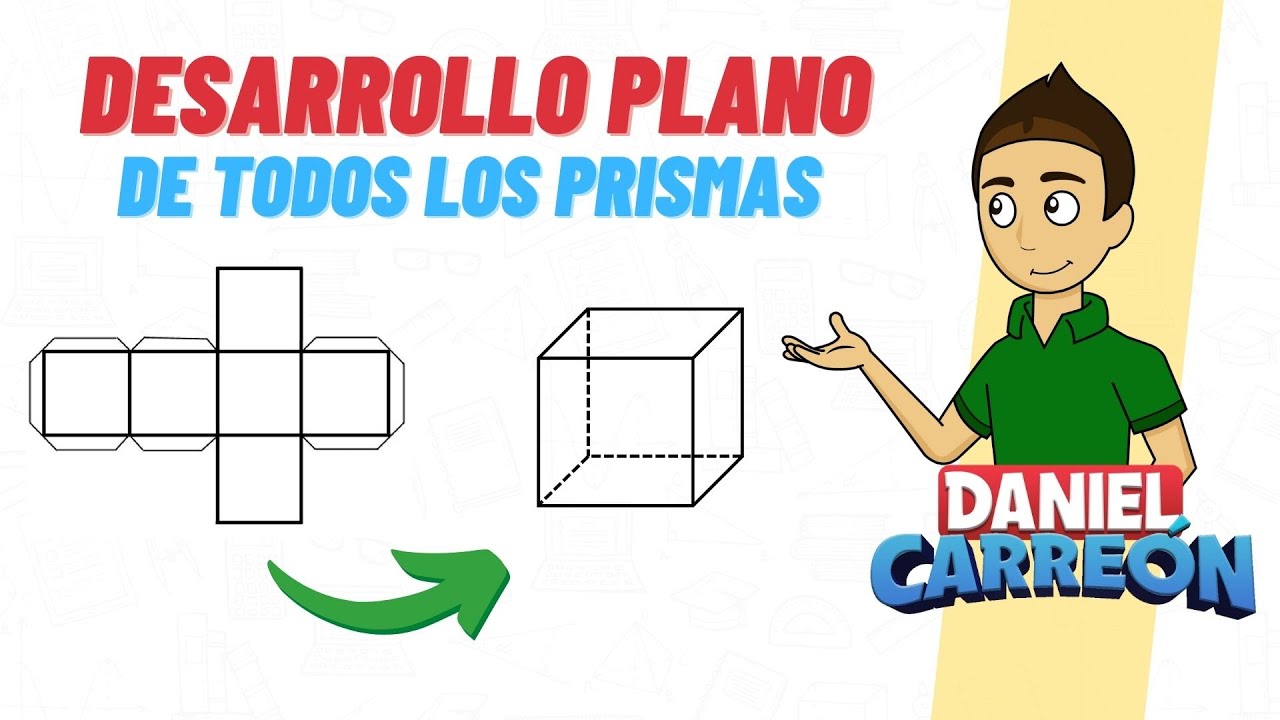
En este artículo, nos sumergiremos en el fascinante mundo geométrico de los cubos, desglosando detalladamente todos sus planos y facetas. Desde las bases hasta las diagonales, exploraremos cada parte de este sólido tridimensional con curiosidad y asombro.
La estructura básica de un cubo
Para comprender a fondo un cubo, es esencial tener una comprensión clara de su estructura básica. Un cubo es un poliedro con seis caras cuadradas iguales, ocho vértices y doce aristas. Está formado por tres ejes perpendiculares entre sí, lo que le otorga una simetría única.
Las caras de un cubo
Cada una de las seis caras de un cubo es un cuadrado perfecto, lo que significa que todos sus lados tienen la misma longitud y todos sus ángulos son de 90 grados. Estas caras forman las superficies externas del cubo y son fundamentales para su estructura.
Las aristas del cubo
Las aristas de un cubo son las líneas donde se encuentran dos caras contiguas. Cada cubo tiene un total de doce aristas, cada una formada por la intersección de dos caras cuadradas. Estas aristas definen la forma del cubo y le proporcionan su rigidez característica.
Las dimensiones de un cubo
La altura, el ancho y la profundidad son las tres dimensiones de un cubo. Estas medidas son iguales en un cubo perfecto y determinan su tamaño total. La formula para calcular el volumen de un cubo es V = a^3, donde ‘a’ representa la longitud de un lado del cubo.
Los vértices del cubo
Los vértices de un cubo son los puntos donde convergen las aristas. En un cubo, hay un total de ocho vértices, cada uno representando el punto de unión de tres aristas. Estos vértices son fundamentales para definir la forma y la estructura tridimensional del cubo.
Las diagonales de un cubo
Cada cara de un cubo tiene dos diagonales que se extienden desde vértices opuestos. Estas diagonales atraviesan el centro de la cara y se cruzan en ángulos rectos. Las diagonales de un cubo son importantes para determinar distancias y ángulos dentro de su estructura.
La geometría interna de un cubo
Adentrándonos en el interior de un cubo, descubrimos una serie de elementos geométricos fascinantes. Desde las líneas proyectadas hasta los puntos de fuga, la geometría interna de un cubo revela un orden y una belleza intrincados.
Las proyecciones ortogonales en un cubo
Las proyecciones ortogonales son representaciones bidimensionales de un objeto tridimensional. En el caso de un cubo, las proyecciones ortogonales muestran sus caras y aristas desde diferentes ángulos, permitiendo una visión detallada de su estructura interna.
Los ángulos internos de un cubo
Los ángulos internos de un cubo juegan un papel crucial en su geometría interna. Cada vértice de un cubo tiene angulos internos que suman 360 grados, lo que refleja la regularidad y simetría de este sólido tridimensional.
Aplicaciones prácticas de los cubos
Además de su valor geométrico y estético, los cubos tienen una amplia gama de aplicaciones prácticas en el mundo real. Desde la construcción de edificios hasta la creación de algoritmos, la versatilidad de los cubos los convierte en objetos de interés en diversos campos.
La representación visual de un cubo
La representación visual de un cubo en dos dimensiones es un desafío artístico y técnico. Los artistas y diseñadores utilizan técnicas de perspectiva y sombreado para dar la ilusión de profundidad y volumen a un cubo en un plano bidimensional.
La utilización de cubos en la programación
En el ámbito de la programación informática, los cubos se utilizan como elementos fundamentales en la creación de algoritmos y estructuras de datos. La representación tridimensional de datos en forma de cubos facilita la visualización y el análisis de información compleja.
Explorando la belleza matemática de los cubos
Desde la antigüedad, los matemáticos han quedado fascinados por la simetría y la regularidad de los cubos. La geometría de los cubos ha inspirado teoremas, axiomas y enigmas que desafían la mente y estimulan la creatividad.
Los patrones geométricos en los cubos
Los patrones geométricos que emergen de los cubos son un campo de estudio fascinante en las matemáticas. Desde los fractales hasta las secuencias numéricas, los cubos ofrecen una riqueza de patrones y estructuras que despiertan la curiosidad de los investigadores.
La influencia de los cubos en la geometría abstracta
En la geometría abstracta, los cubos se utilizan como elementos fundamentales para explorar conceptos como la simetría, la transformación y la topología. La estructura regular y predecible de un cubo lo convierte en un objeto de estudio invaluable en este campo matemático.
¿Cuál es la fórmula para calcular el volumen de un cubo?
La fórmula para calcular el volumen de un cubo es V = a^3, donde ‘a’ representa la longitud de un lado del cubo.
¿Cuántos vértices tiene un cubo?
Un cubo tiene un total de ocho vértices, cada uno representando el punto de unión de tres aristas.