Cuando se trata de figuras geométricas, los polígonos son fascinantes estructuras que nos desafían a explorar diferentes aspectos matemáticos. En este artículo, nos sumergiremos en el mundo del pentágono y descubriremos la suma de sus ángulos internos.
El misterio detrás de los ángulos internos de un pentágono
¿Alguna vez te has preguntado por qué la suma de los ángulos internos de un pentágono es tan peculiar en comparación con otras formas geométricas?
Definición de un pentágono
Para comprender la suma de los ángulos internos de un pentágono, primero debemos definir qué es un pentágono. Un pentágono es un polígono que tiene cinco lados y cinco ángulos.
Ángulos de un pentágono regular
¿Sabías que un pentágono regular es una figura en la que todos los lados son iguales y todos los ángulos internos tienen la misma medida?
Medida de los ángulos internos de un pentágono regular
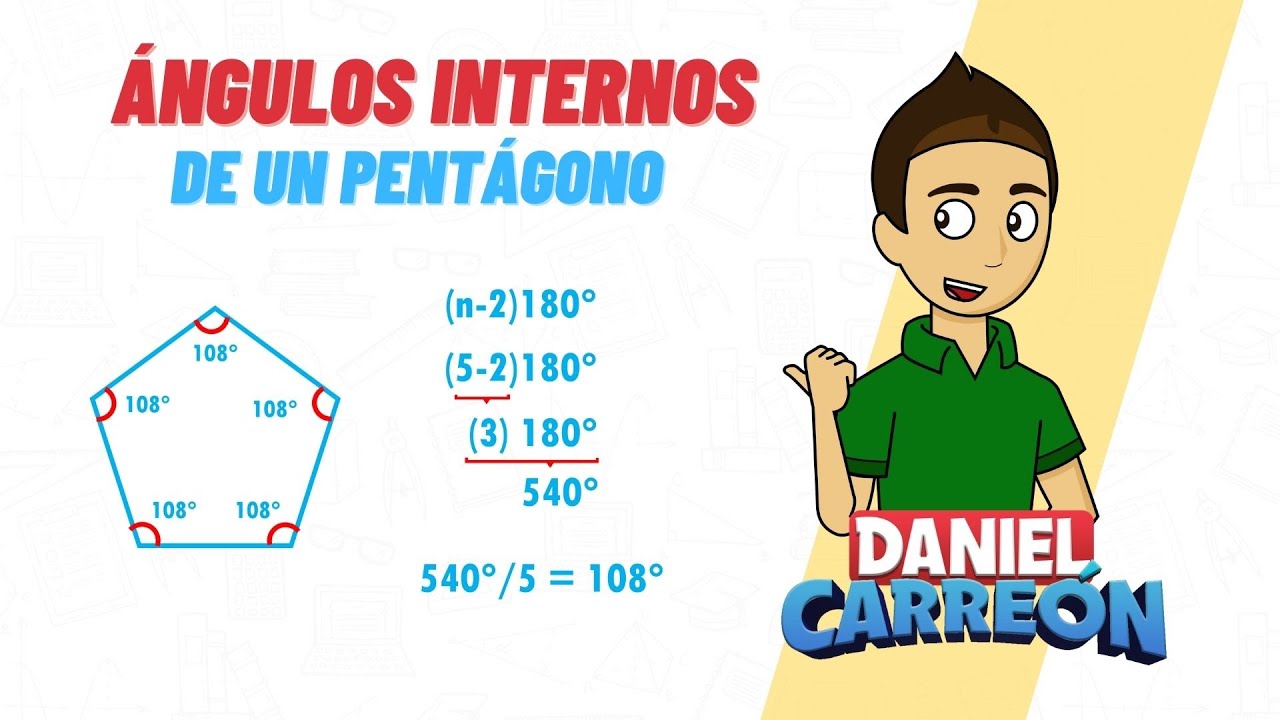
En un pentágono regular, cada ángulo interno mide 108 grados. Si sumamos los ángulos internos de un pentágono regular, obtenemos un total de 540 grados. Esta característica única del pentágono lo distingue de otras figuras geométricas y lo convierte en un objeto de estudio intrigante.
La fórmula mágica detrás de la suma de los ángulos internos
Fórmula general para encontrar la suma de ángulos internos
Para cualquier polígono, no solo el pentágono, la fórmula para hallar la suma de los ángulos internos es: (n-2) x 180 grados, donde «n» representa el número de lados del polígono. Aplicando esta fórmula al pentágono, con n=5, obtenemos:
(5-2) x 180 = 3 x 180 = 540 grados
Esta fórmula se puede usar para demostrar la suma de ángulos internos para cualquier polígono, lo que permite una comprensión más profunda de la geometría y sus propiedades.
Aplicaciones prácticas de la suma de ángulos internos de un pentágono
En la arquitectura y el diseño
¿Te has preguntado cómo los arquitectos y diseñadores utilizan el conocimiento de la suma de ángulos internos de un pentágono en sus creaciones?
Distribución espacial
Al comprender la geometría de un pentágono, los profesionales pueden diseñar estructuras que aprovechan de manera eficiente el espacio y la estética. El conocimiento de cómo se distribuyen los ángulos internos dentro de un pentágono puede influir en la disposición de espacios arquitectónicos de manera armoniosa.
Patrones decorativos
Los patrones decorativos basados en la forma de un pentágono hacen uso de las propiedades de sus ángulos internos para lograr diseños visualmente atractivos y simétricos. Esta conexión entre la geometría y el arte ha sido explorada a lo largo de la historia en diversas culturas.
En matemáticas avanzadas
¿Qué relevancia tienen los ángulos internos de un pentágono en campos matemáticos más avanzados?
Geometría fractal
El estudio de fractales y geometría fractal puede involucrar conceptos relacionados con la geometría de polígonos, incluidos los pentágonos. La comprensión de la geometría de los ángulos internos de un pentágono puede sentar las bases para exploraciones más complejas en el mundo de la geometría fractal.
Trigonometría y cálculos avanzados
En el campo de la trigonometría y los cálculos matemáticos avanzados, los ángulos internos de un pentágono pueden ser parte de cálculos más elaborados que requieren un profundo conocimiento de las propiedades geométricas. Estas aplicaciones muestran cómo los conceptos simples de geometría pueden extenderse a campos matemáticos más sofisticados.
¿La suma de los ángulos internos de un pentágono siempre es la misma?
Absolutamente, la suma de los ángulos internos de un pentágono regular siempre será de 540 grados debido a la distribución uniforme de los ángulos en esta figura geométrica.
¿Se puede aplicar la fórmula de los ángulos internos a otros polígonos?
Sí, la fórmula (n-2) x 180 grados es una regla general que se aplica a cualquier polígono, lo que facilita la comprensión de la geometría en diferentes contextos.
¿Por qué es importante comprender la suma de ángulos internos de un pentágono?
La comprensión de la geometría de un pentágono y la suma de sus ángulos internos no solo nos permite explorar las propiedades matemáticas, sino que también tiene aplicaciones prácticas en diversos campos como el diseño, la arquitectura y las matemáticas avanzadas.
¡Espero que este viaje por el mundo de los ángulos internos de un pentágono haya sido tan fascinante para ti como lo fue para mí al escribirlo!