¿Alguna vez te has detenido a observar la belleza de la simetría en el mundo que nos rodea? La simetría es un concepto fascinante que se encuentra en todas partes, desde las estructuras naturales hasta las creaciones humanas. En el campo de las matemáticas, la simetría axial juega un papel crucial al ayudarnos a comprender y visualizar patrones, formas y relaciones geométricas.
¿Qué es la simetría axial?
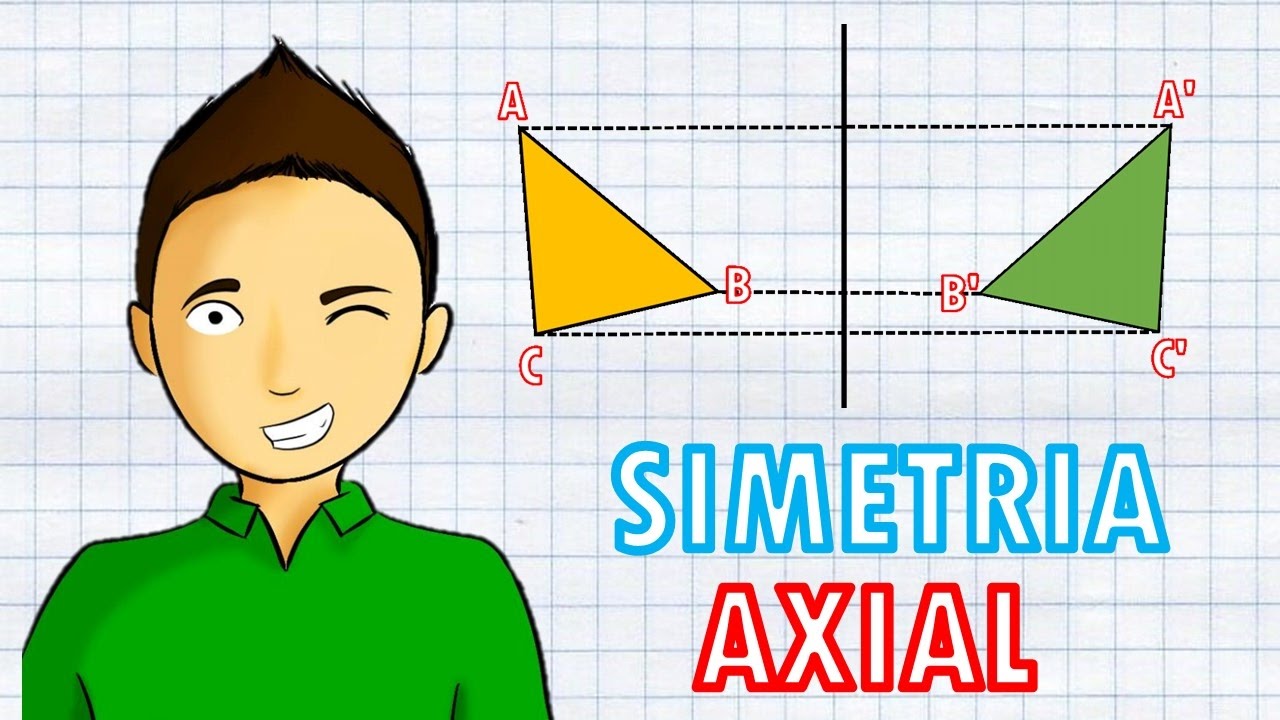
La simetría axial, también conocida como simetría de reflexión, es un tipo de simetría en la que un objeto se refleja en un eje imaginario para coincidir exactamente consigo mismo. Este eje de simetría es una línea recta que divide al objeto en dos partes iguales y simétricas. Visualmente, podemos pensar en este proceso como si estuviéramos mirando un objeto en un espejo.
Características de la simetría axial
En la simetría axial, cada punto del objeto original tiene un punto correspondiente en la imagen reflejada a la misma distancia del eje de simetría pero en la dirección opuesta. Esta propiedad garantiza que las distancias y ángulos relativos entre los puntos del objeto se conserven en la imagen reflejada, lo que crea una reproducción especular precisa del objeto original.
Aplicaciones de la simetría axial
La simetría axial no solo es un concepto teórico interesante en matemáticas, sino que también tiene numerosas aplicaciones prácticas en áreas como el diseño gráfico, la arquitectura y la ingeniería. Por ejemplo, en el diseño de logotipos o edificios, la simetría axial se utiliza para crear composiciones estéticamente agradables y equilibradas.
Propiedades matemáticas de la simetría axial
Eje de simetría
El eje de simetría en la simetría axial es una línea recta que actúa como un punto de referencia alrededor del cual se produce la reflexión del objeto. Esta línea divide al objeto en dos partes idénticas y opuestas, lo que garantiza que la simetría se mantenga en todas las direcciones a lo largo del eje.
Puntos invariantes
Los puntos invariantes son aquellos puntos en un objeto que no cambian de posición durante la reflexión. En la simetría axial, estos puntos son puntos equidistantes del eje de simetría en el objeto original y en su imagen reflejada.
Composición de figuras
Una de las fascinantes propiedades de la simetría axial es su capacidad para componer figuras complejas a partir de elementos más simples. Al reflejar y combinar patrones básicos a lo largo de un eje de simetría, podemos crear diseños intrincados y armoniosos que capturan la esencia de la simetría en su máxima expresión.
Importancia de la simetría axial en matemáticas
Intuición geométrica
La simetría axial es fundamental para desarrollar una sólida intuición geométrica, ya que nos permite visualizar y comprender las transformaciones espaciales de manera más clara. Al identificar y trabajar con simetrías en formas y figuras, fortalecemos nuestra capacidad de análisis y resolución de problemas matemáticos.
Relaciones matemáticas
En matemáticas, la simetría axial también está estrechamente relacionada con conceptos como los números negativos, la ecuación de una recta y las funciones pares e impares. Estas conexiones profundizan nuestra comprensión de la simetría en un contexto más amplio y nos permiten aplicar sus principios en diversos ámbitos matemáticos.
Desafío matemático: patrones simétricos
¿Te gustaría poner a prueba tus habilidades matemáticas y creativas al mismo tiempo? Intenta crear patrones simétricos utilizando la simetría axial. Empieza dibujando una figura sencilla y luego aplica reflexiones a lo largo de un eje de simetría para expandir y transformar tu diseño en una composición simétrica única.
¿La simetría axial es lo mismo que la simetría radial?
No, la simetría axial y la simetría radial son dos tipos diferentes de simetría. Mientras que la simetría axial implica una reflexión en un eje, la simetría radial implica una rotación alrededor de un punto central.
¿Por qué es importante estudiar la simetría axial en matemáticas?
Estudiar la simetría axial en matemáticas ayuda a desarrollar habilidades de pensamiento visual, así como a profundizar la comprensión de conceptos geométricos fundamentales. Además, la simetría axial tiene aplicaciones prácticas en diversos campos, lo que la convierte en un principio matemático relevante y versátil.
¿Cómo se relaciona la simetría axial con la arquitectura y el diseño?
La simetría axial se utiliza ampliamente en la arquitectura y el diseño para crear estructuras equilibradas y estéticamente agradables. Al aplicar principios de simetría axial, los arquitectos y diseñadores pueden lograr composiciones visuales armoniosas que resuenan con la belleza y la coherencia matemática.