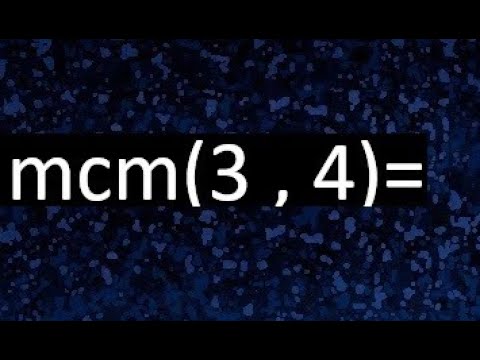El Mínimo Común Múltiplo (MCM) es un concepto fundamental en matemáticas que nos permite encontrar el número más pequeño que es múltiplo de dos o más números. En este caso, nos enfocaremos en encontrar el MCM de los números 4 y 3.
La importancia del Mínimo Común Múltiplo
El MCM es crucial en diversas situaciones matemáticas y prácticas cotidianas. ¿Te has preguntado por qué es tan relevante encontrar el MCM de un conjunto de números? Bueno, imagina que necesitas dividir un pastel en partes iguales para compartir con tus amigos. Para lograrlo de manera justa, debes conocer el MCM de las porciones en las que deseas dividir el pastel.
¿Qué es el Mínimo Común Múltiplo?
El MCM, como su nombre indica, es el menor múltiplo común entre dos o más números. En el caso específico de los números 4 y 3, el MCM es el valor más pequeño que ambos comparten como múltiplo. Para calcular el MCM de 4 y 3, primero necesitamos desglosar estos números en sus factores primos.
Descomposición en factores primos
Para encontrar el MCM de 4 y 3, descompondremos cada número en sus factores primos. Es importante recordar que un número primo es aquel que solo es divisible por 1 y por sí mismo. En el caso de 4 y 3:
Descomposición de 4
El número 4 puede descomponerse en sus factores primos como 2 x 2, ya que 2 es un número primo y es el único factor primo de 4. Por lo tanto, la descomposición de 4 en factores primos es 2².
Descomposición de 3
Por otro lado, el número 3 es primo, por lo que su descomposición en factores primos es simplemente él mismo, es decir, 3.
Calculando el Mínimo Común Múltiplo
Una vez que tenemos la descomposición en factores primos de 4 y 3, podemos calcular el MCM. Para ello, tomamos los factores primos comunes y no comunes con su mayor exponente común. En este caso:
Los factores primos comunes son 2 (ya que ambos números tienen un factor primo de 2).
Los factores primos no comunes son 2 y 3.
El MCM se calcula multiplicando los factores comunes y no comunes elevados a sus mayores exponentes: MCM(4, 3) = 2² x 3 = 12.
Resultado y Aplicaciones Prácticas
Por lo tanto, el MCM de 4 y 3 es 12. Este resultado es fundamental en situaciones donde se deben encontrar patrones recurrentes en eventos periódicos o calcular fracciones equivalentes. Saber cómo obtener el MCM te permitirá simplificar cálculos complejos y optimizar procesos en diversos contextos.
¿Por qué es esencial conocer el MCM?
Conocer el MCM es esencial para simplificar operaciones matemáticas, dividir cantidades en partes iguales y encontrar fracciones equivalentes de manera eficiente.
¿Cuál es la relación entre el MCM y el máximo común divisor (MCD)?
El MCM y el MCD son conceptos complementarios en aritmética. Mientras el MCM busca el mínimo múltiplo común, el MCD busca el mayor divisor común entre dos o más números.
¿Existen métodos alternativos para calcular el MCM?
Sí, existen diferentes métodos para calcular el MCM, como el método de descomposición en factores primos o el método de listas de factores. Es importante elegir el método que mejor se adapte a la situación problemática.