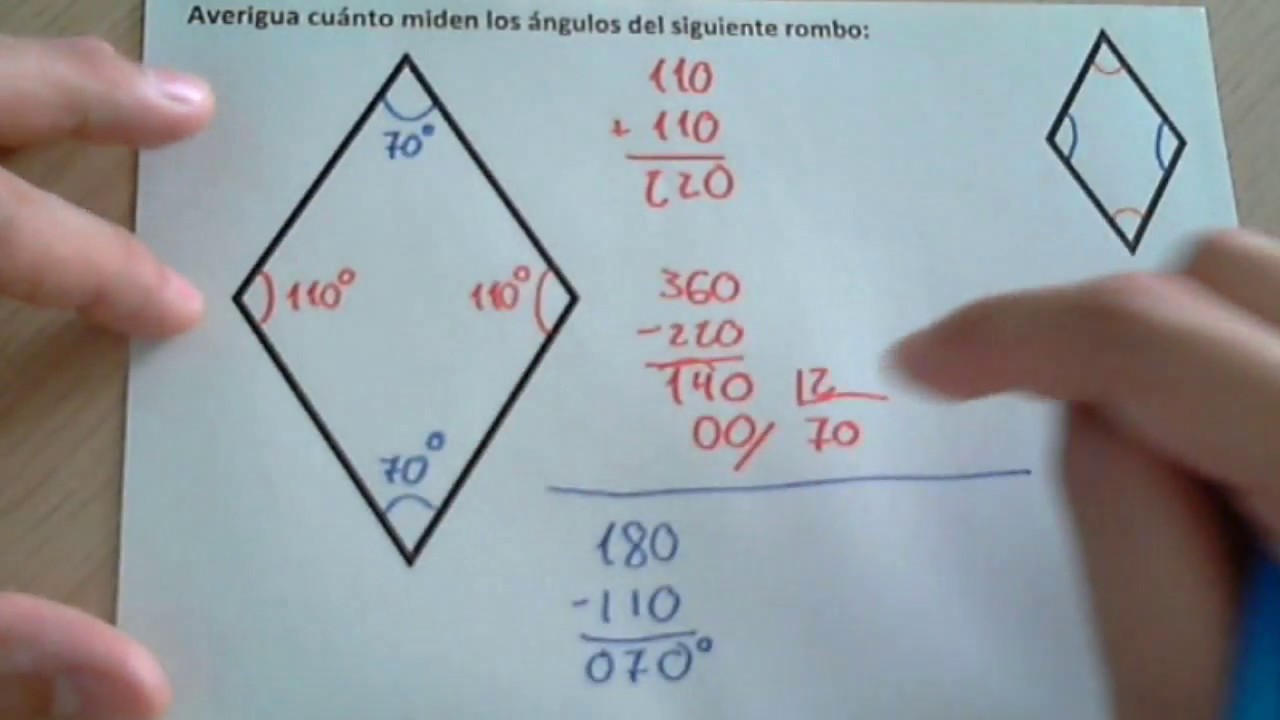
Un rombo es un tipo de cuadrilátero con propiedades geométricas especiales, incluidos sus ángulos internos. Comprender las medidas de ángulos en un rombo es fundamental para resolver problemas de geometría y aplicar conceptos matemáticos en situaciones cotidianas.
Ángulos en un rombo: Características principales
En un rombo, los cuatro lados son iguales en longitud, lo que implica que los ángulos internos también tienen valores específicos. Los ángulos opuestos en un rombo son congruentes, lo que significa que tienen la misma medida. Esta característica única es clave para determinar las medidas de los ángulos en un rombo de forma eficiente.
Ángulo agudo en un rombo
Uno de los ángulos en un rombo es un ángulo agudo, que tiene una medida menor a 90 grados. Este ángulo es crucial para la simetría y la estructura del rombo, ya que se relaciona con sus diagonales y propiedades geométricas intrínsecas.
Ángulos obtusos en un rombo
Los otros tres ángulos en un rombo son ángulos obtusos, con medidas mayores a 90 grados. Estos ángulos también desempeñan un papel significativo en la geometría del rombo, y su relación con el ángulo agudo es fundamental para entender la forma y el tamaño del rombo en su totalidad.
Cálculo de las medidas de ángulos en un rombo
Para determinar las medidas específicas de los ángulos en un rombo, se pueden aplicar diversas fórmulas y conceptos geométricos. Es fundamental comprender la relación entre los ángulos internos y sus propiedades geométricas para resolver problemas con precisión.
La suma de los ángulos internos de un rombo
La suma de los ángulos internos de cualquier cuadrilátero, incluido un rombo, es siempre igual a 360 grados. Esta propiedad es esencial para abordar problemas que involucran múltiples ángulos en un rombo y verificar la precisión de los cálculos realizados.
Fórmulas para hallar los ángulos en un rombo
Existen fórmulas específicas para encontrar la medida de cada ángulo individual en un rombo, considerando sus propiedades geométricas únicas y la relación entre los ángulos opuestos. Estas fórmulas facilitan la resolución de problemas matemáticos que implican ángulos en un rombo.
Aplicaciones prácticas de los ángulos en un rombo
Los conceptos relacionados con los ángulos en un rombo tienen aplicaciones prácticas en diferentes campos, como la arquitectura, el diseño, la ingeniería y la geografía. Comprender cómo calcular y utilizar las medidas de ángulos en un rombo puede ser beneficioso en diversas situaciones cotidianas.
Diseño arquitectónico basado en ángulos en un rombo
En arquitectura, los ángulos en un rombo pueden influir en la creación de estructuras simétricas y estéticamente agradables. La cuidadosa consideración de los ángulos internos de un rombo puede resultar en diseños únicos y funcionales que aprovechan al máximo las propiedades geométricas del rombo.
Aplicaciones en la ingeniería y la geografía
En ingeniería y geografía, comprender las medidas de ángulos en un rombo es fundamental para la planificación de proyectos, la delimitación de áreas y la resolución de problemas espaciales complejos. La precisión en el cálculo de ángulos en un rombo puede influir en la eficacia y la viabilidad de diversas iniciativas.
Explorando la belleza matemática de los ángulos en un rombo
Los ángulos en un rombo no solo son entidades geométricas abstractas, sino que también reflejan la armonía y la elegancia presentes en las formas geométricas. La simetría y precisión de los ángulos en un rombo pueden ser apreciadas por su belleza matemática y su relevancia en múltiples disciplinas.
Metáfora de los ángulos en un rombo
Imagina los ángulos en un rombo como las piezas de un rompecabezas matemático que se encajan perfectamente para formar una imagen completa y coherente. Cada ángulo en un rombo contribuye a la estructura global, de la misma manera en que cada detalle en una obra de arte contribuye a su impacto visual.
Exploración creativa de los ángulos en un rombo
Invita a tu creatividad a jugar con los ángulos en un rombo, observando patrones, simetrías y relaciones para descubrir nuevas perspectivas y enfoques en matemáticas y geometría. La exploración creativa de los ángulos en un rombo puede inspirar innovación y pensamiento lateral en diversos contextos.
¿Por qué son importantes los ángulos en un rombo?
Los ángulos en un rombo son importantes porque determinan la forma y la simetría de esta figura geométrica, lo que a su vez tiene implicaciones en diversas áreas como la arquitectura y la ingeniería.
¿Cómo se calculan los ángulos en un rombo?
Los ángulos en un rombo se pueden calcular utilizando fórmulas específicas que tienen en cuenta las propiedades únicas de esta figura, como la igualdad de los lados y la congruencia de los ángulos opuestos.
¿Qué aplicaciones prácticas tienen los ángulos en un rombo en la vida cotidiana?
Los ángulos en un rombo tienen aplicaciones en campos como la arquitectura, la cartografía y la planificación urbana al contribuir a la creación de estructuras sólidas y diseños funcionales.