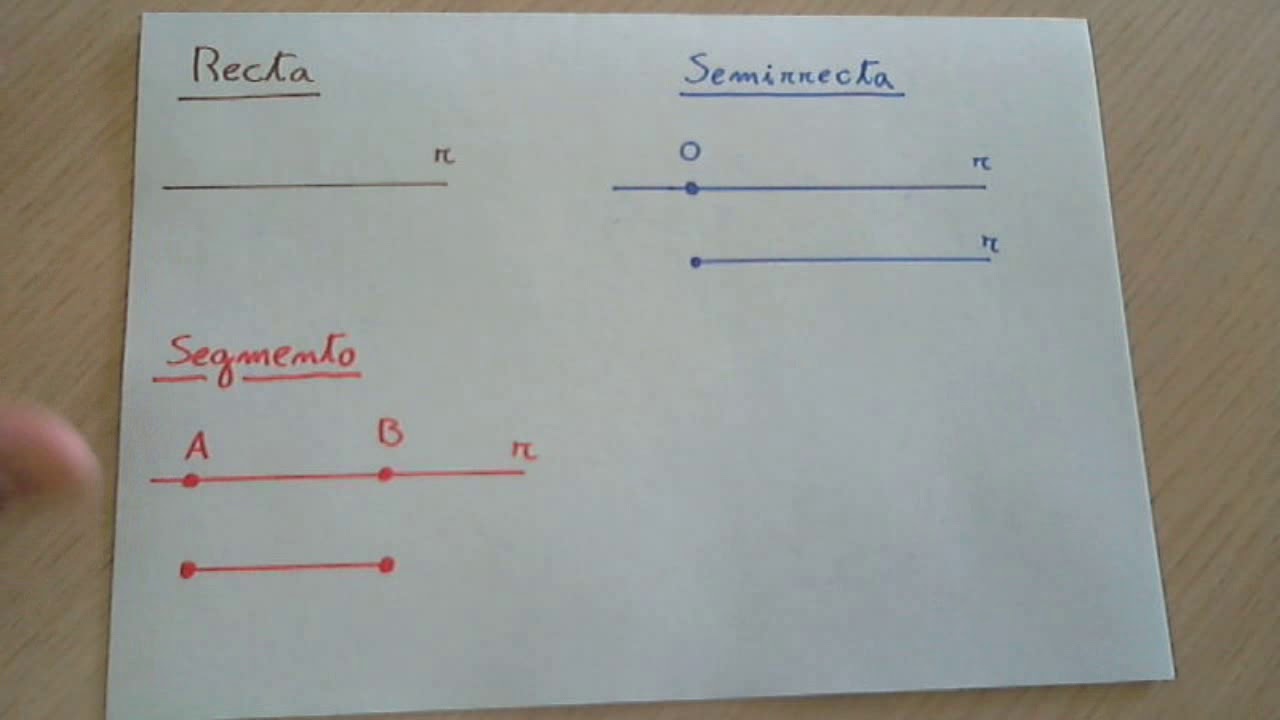
Para comprender verdaderamente la geometría y sus distintos elementos, es fundamental diferenciar entre un segmento de recta y una semirrecta. A menudo, estos conceptos pueden generar confusión, pero en realidad presentan diferencias significativas en su definición y aplicación.
Definición de un segmento de recta
Un segmento de recta es una parte de una recta limitada por dos puntos finitos, denominados extremos. Es importante destacar que un segmento de recta tiene una longitud definida y claramente delimitada por los puntos que lo establecen. Esta característica lo distingue de otros elementos geométricos que pueden extenderse indefinidamente en ambas direcciones.
Características de un segmento de recta
Un segmento de recta es una entidad geométrica que no tiene dimensiones, es decir, no tiene ancho ni profundidad, solo longitud. Esta propiedad lo convierte en una herramienta fundamental en la geometría para medir distancias y establecer relaciones espaciales entre puntos.
Uso de segmentos de recta en geometría analítica
En el ámbito de la geometría analítica, los segmentos de recta son representados mediante ecuaciones matemáticas que involucran coordenadas en un plano cartesiano. Estas representaciones permiten realizar cálculos precisos y resolver problemas geométricos de manera sistemática.
Definición de una semirrecta
Por otro lado, una semirrecta es una porción de una recta que tiene un punto de origen pero se extiende indefinidamente en una sola dirección. A diferencia de un segmento de recta, una semirrecta no tiene un extremo final, lo que le otorga una naturaleza ilimitada en una única dirección.
Características de una semirrecta
Una semirrecta parte de un punto específico, denominado origen, y se extiende indefinidamente en una sola dirección. Esta propiedad la hace útil en contextos donde es necesario indicar una dirección concreta sin establecer un límite final.
Aplicaciones de las semirrectas en trigonometría
En trigonometría, las semirrectas son empleadas para representar ángulos en un plano, creando líneas dirigidas que facilitan el cálculo de medidas angulares y la resolución de problemas trigonométricos.
Diferencias clave entre un segmento de recta y una semirrecta
Aunque tanto los segmentos de recta como las semirrectas son parte de la geometría euclidiana básica, presentan diferencias fundamentales que es crucial tener en cuenta:
Longitud definida vs. Extensión ilimitada
La principal diferencia radica en que un segmento de recta tiene una longitud definida y limitada entre dos puntos, mientras que una semirrecta se extiende indefinidamente en una sola dirección sin tener un extremo final.
Uso en cálculos geométricos
Los segmentos de recta son comúnmente utilizados para medir distancias y realizar cálculos precisos en geometría, mientras que las semirrectas son útiles para marcar direcciones específicas de manera ilimitada.
Representación matemática
En la representación matemática, los segmentos de recta son definidos por dos puntos concretos, mientras que las semirrectas requieren un origen específico desde el cual se extienden indefinidamente en una sola dirección.
En definitiva, comprender la diferencia entre un segmento de recta y una semirrecta es esencial para abordar adecuadamente problemas geométricos y matemáticos que requieren la precisión en la delimitación de medidas y direcciones. Ambos conceptos, aunque relacionados, cumplen funciones distintas y complementarias en el estudio de la geometría.
¿Por qué es importante distinguir entre un segmento de recta y una semirrecta?
La diferenciación entre estos conceptos permite establecer límites claros en problemas geométricos y matemáticos, evitando confusiones en la medición de distancias y la indicación de direcciones.
¿Qué papel juegan los segmentos de recta y las semirrectas en la trigonometría?
En trigonometría, tanto los segmentos de recta como las semirrectas son fundamentales para representar ángulos y generar mediciones precisas que facilitan el cálculo trigonométrico en distintos contextos.
¡Espero que este artículo te haya sido de utilidad para comprender las diferencias entre un segmento de recta y una semirrecta!