¿Alguna vez te has preguntado cuáles son las partes de la raíz cuadrada y cómo funciona este concepto matemático tan fascinante? En este artículo, te llevaremos a un viaje a través de los aspectos más profundos de la raíz cuadrada, desglosando cada componente para que puedas entenderlo de manera clara y sencilla.
Desmitificando la Notación de la Raíz Cuadrada
Antes de sumergirnos en las partes específicas de la raíz cuadrada, es crucial comprender la notación que la rodea. La raíz cuadrada se representa por el símbolo √, que indica la operación matemática inversa del cuadrado, es decir, encontrar el número que, multiplicado por sí mismo, da como resultado el valor bajo el signo radical.
Componentes Básicos de una Raíz Cuadrada
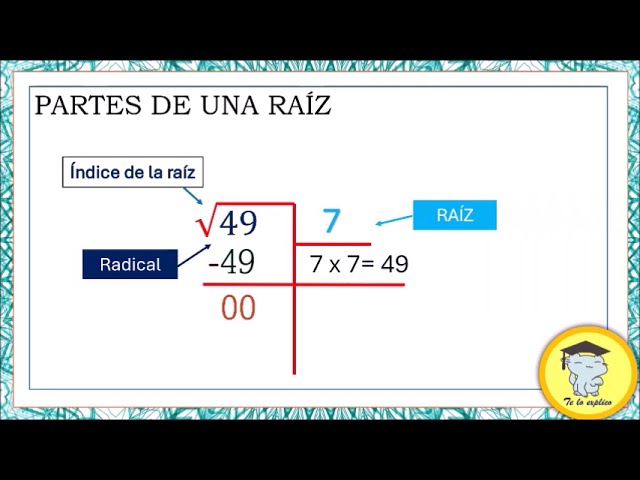
Para comprender completamente la raíz cuadrada, debemos desglosarla en sus partes fundamentales. El primer elemento a considerar es el radicando, que es el número bajo el signo de radical y cuya raíz estamos buscando. Por ejemplo, en la raíz cuadrada de 16, el 16 es el radicando.
El Radical y el Índice
Además del radicando, la raíz cuadrada también incluye el radical, que es el símbolo √, y el índice, que en el caso de la raíz cuadrada es 2. El índice indica la raíz que se está calculando; en este caso, al ser 2, estamos buscando la raíz cuadrada. Por lo tanto, cuando se menciona la raíz cuadrada, nos referimos a la raíz de índice 2.
La Importancia del Signo Radical
El signo radical no solo es un símbolo visual en la expresión matemática, sino que también indica la presencia de una raíz, ayudando a diferenciarla de otras operaciones. Es esencial prestar atención al radical para interpretar correctamente la operación matemática que se está llevando a cabo.
Aplicaciones de la Raíz Cuadrada en la Vida Cotidiana
Aunque la raíz cuadrada puede parecer un concepto puramente matemático, su utilidad se extiende a situaciones muy comunes en nuestra vida diaria. Desde calcular distancias hasta determinar áreas en la geometría, la raíz cuadrada juega un papel crucial en diversos contextos prácticos.
Cálculo de Distancias con la Raíz Cuadrada
Imagina que necesitas averiguar la longitud de un lado de un cuadrado dado su área total. Aquí es donde entra en juego la raíz cuadrada, ya que al calcularla, puedes encontrar el valor exacto de un lado del cuadrado a partir de su área, lo que resulta útil en arquitectura, carpintería y otras disciplinas que requieren mediciones precisas.
Raíces Cuadradas en Geometría
En la geometría, la raíz cuadrada se utiliza para determinar las longitudes de los lados de un cuadrado perfecto conociendo su área. Esta aplicación demuestra cómo los conceptos matemáticos, como las raíces cuadradas, tienen una relevancia directa en la representación y medición de figuras geométricas en el espacio tridimensional.
Curiosidades y Usos Avanzados de la Raíz Cuadrada
La raíz cuadrada va más allá de simples cálculos y se adentra en ámbitos más complejos y sorprendentes. Desde aplicaciones en música hasta en el ámbito tecnológico, este concepto matemático tiene un alcance que va mucho más allá de lo que podríamos imaginar.
Música y Raíces Cuadradas
¿Sabías que las raíces cuadradas también tienen su lugar en el mundo de la música? En la teoría musical, las raíces cuadradas se utilizan en la construcción de escalas microtonales, que exploran intervalos de sonido más pequeños que los tradicionales, añadiendo complejidad y riqueza al arte sonoro.
Avances Tecnológicos Impulsados por la Raíz Cuadrada
En el ámbito tecnológico, la raíz cuadrada se aplica en algoritmos y cálculos avanzados, como en la mejora de la precisión de los sistemas de navegación por satélite o en la compresión de datos para almacenamiento eficiente. Estos usos muestran cómo un concepto matemático básico puede tener un impacto significativo en el desarrollo de tecnologías actuales.
Preguntas Frecuentes sobre la Raíz Cuadrada
¿Qué sucede si el radicando es un número negativo en la raíz cuadrada?
En el contexto de la raíz cuadrada, si el radicando es un número negativo, el resultado suele ser un número complejo, ya que no existe un número real que, al ser elevado al cuadrado, dé un valor negativo. Los números complejos permiten trabajar con raíces cuadradas de números negativos y amplían el ámbito de las operaciones matemáticas.
¿Cómo puedo calcular mentalmente una raíz cuadrada sin una calculadora?
Calcular mentalmente una raíz cuadrada puede ser un desafío, pero existen técnicas como el método de estimación por aproximaciones sucesivas que permiten obtener una aproximación de la raíz cuadrada de un número sin la necesidad de una calculadora. Dividir el número en segmentos más pequeños y buscar cuadrados perfectos cercanos son estrategias útiles para realizar cálculos mentales de raíces cuadradas.
¿Por qué es importante comprender la raíz cuadrada en la educación matemática?
La comprensión de la raíz cuadrada no solo amplía el repertorio de herramientas matemáticas de una persona, sino que también fomenta el pensamiento crítico y la resolución de problemas. Al dominar conceptos como las raíces cuadradas, los estudiantes desarrollan habilidades matemáticas fundamentales que son aplicables en diversos campos académicos y profesionales.