Descubriendo la simetría en los cuadrados
¡Bienvenidos, curiosos de las figuras geométricas! En este artículo exploraremos el fascinante mundo de la simetría en relación con uno de los polígonos más conocidos: el cuadrado. ¿Alguna vez te has preguntado cuántos ejes de simetría tiene un cuadrado? ¡Acompáñanos en este viaje de descubrimiento matemático!
El concepto de simetría en geometría
Antes de sumergirnos en los detalles de los cuadrados, es esencial comprender qué es la simetría en el contexto de la geometría. La simetría se refiere a la cualidad de una figura geométrica de conservar su forma, tamaño y posición original después de aplicar ciertas transformaciones. Estas transformaciones pueden incluir reflexiones, rotaciones y traslaciones. La simetría es una propiedad fundamental que se puede apreciar en numerosos objetos y estructuras en el mundo que nos rodea.
Los cuadrados: figuras simétricas por excelencia
Los cuadrados son polígonos con cuatro lados de igual longitud y cuatro ángulos rectos. Su apariencia regular y equilibrada los convierte en figuras altamente simétricas, lo que los hace especialmente interesantes para explorar los conceptos de simetría. ¿Pero cuántos ejes de simetría tiene un cuadrado? ¡Continúa leyendo para descubrirlo!
Definiendo un eje de simetría
Antes de abordar el número de ejes de simetría de un cuadrado, es crucial entender qué es exactamente un eje de simetría. En términos simples, un eje de simetría es una línea imaginaria alrededor de la cual una figura puede ser reflejada para que coincida consigo misma. Esto significa que si aplicamos una reflexión a la figura a lo largo de su eje de simetría, la figura original y su imagen reflejada se superponen perfectamente.
Los cuadrados y sus ejes de simetría
Los cuadrados son fascinantes por varias razones, entre ellas su simetría inherente. Al analizar un cuadrado, notamos que tiene múltiples ejes de simetría que juegan un papel crucial en su estructura geométrica. ¿Estás listo para descubrir cuántos ejes de simetría tiene un cuadrado?
Ejes de simetría de un cuadrado
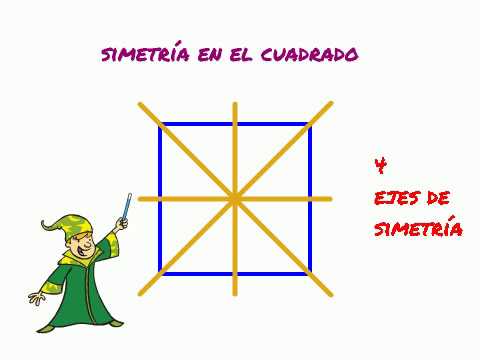
Un cuadrado posee un total de cuatro ejes de simetría. Sí, ¡has leído bien! Estos ejes atraviesan el centro del cuadrado y conectan sus vértices opuestos. Al trazar estos ejes, podemos observar cómo el cuadrado se divide en secciones simétricas que reflejan la configuración de los lados y ángulos del polígono.
La simetría rotacional del cuadrado
Además de sus ejes de simetría tradicionales, los cuadrados también exhiben una forma especial de simetría conocida como simetría rotacional. Esta simetría implica que un cuadrado puede ser rotado en torno a su centro por múltiplos de 90 grados y seguir luciendo idéntico en cada posición. ¡Imagina girar un cuadrado y observar cómo cada rotación revela la misma forma y estructura intrínseca!
Explorando la versatilidad de la simetría cuadrada
¿Qué más podemos desentrañar sobre la simetría de un cuadrado? A medida que profundizamos en sus propiedades simétricas, descubrimos que la versatilidad del cuadrado como figura geométrica simétrica es verdaderamente sorprendente.
Patrones repetitivos y simetría
Los cuadrados, con su combinación única de ejes de simetría y simetría rotacional, permiten la creación de patrones visuales cautivadores. Al colocar varios cuadrados con diferentes orientaciones, podemos generar diseños simétricos que se repiten en todas direcciones. Este enfoque creativo de la simetría no solo es estéticamente atractivo, sino que también resalta la coherencia y armonía presentes en la naturaleza matemática del cuadrado.
Simetría en la naturaleza y el arte
La simetría del cuadrado no solo tiene aplicaciones teóricas, sino que también se manifiesta en contextos prácticos y artísticos. En la naturaleza, encontramos ejemplos de simetría cuadrada en cristales y estructuras moleculares, donde la disposición regular de los átomos refleja la simetría inherente del cuadrado. Del mismo modo, artistas y diseñadores han utilizado la simetría del cuadrado como fuente de inspiración para crear obras impactantes que despiertan la imaginación y estimulan la percepción visual.
Sumergiéndonos en la simetría cuadrada
Con cada nuevo detalle que exploramos sobre la simetría de los cuadrados, nos adentramos más en un mundo de armonía matemática y belleza estructural. La profundidad de esta figura geométrica aparentemente simple nos invita a reflexionar sobre la importancia de la simetría en diferentes aspectos de nuestras vidas.
La simetría como principio organizador
La presencia de la simetría en los cuadrados nos recuerda cómo la estructura ordenada y equilibrada puede ser un principio organizador tanto en las ciencias naturales como en las expresiones artísticas. La simetría no solo nos atrae visualmente, sino que también nos conecta con un sentido más profundo de cohesión y coherencia en el universo que habitamos.
La simetría como metáfora de armonía
Al contemplar la simetría de los cuadrados, podemos verla como una metáfora de la armonía y equilibrio que buscamos en nuestras vidas. Al igual que los ejes de simetría que unen los opuestos en un cuadrado, la búsqueda de equilibrio entre diferentes aspectos de nuestra existencia puede conducirnos a un estado de plenitud y satisfacción.
¿Los cuadrados tienen más ejes de simetría que los rectángulos?
Aunque tanto los cuadrados como los rectángulos son polígonos rectilíneos, los cuadrados poseen más ejes de simetría debido a su configuración de lados iguales y ángulos rectos. Mientras que un cuadrado tiene cuatro ejes de simetría, un rectángulo tendrá menos debido a sus lados desiguales.
¿Cómo influye la simetría de un cuadrado en las estructuras arquitectónicas?
La simetría del cuadrado ha sido un elemento clave en la arquitectura a lo largo de la historia. Desde antiguas civilizaciones hasta diseños modernos, la regularidad y equilibrio de la simetría cuadrada se han utilizado para crear edificaciones impresionantes que transmiten estabilidad y orden estético.
¿Qué otros polígonos exhiben una simetría similar a la del cuadrado?
Entre los polígonos regulares, el hexágono es otro ejemplo de figura con una simetría notablemente similar a la del cuadrado. Ambos polígonos exhiben una combinación de ejes de simetría rectangulares y simetría rotacional que los convierten en estructuras geométricas cautivadoras.
¡Esperamos que este viaje por la simetría de los cuadrados haya sido tan enriquecedor para ti como lo fue para nosotros al escribirlo! La belleza de la simetría geométrica nos invita a apreciar la armonía presente en las formas cotidianas que nos rodean. ¿Listo para explorar más maravillas matemáticas? El mundo de la geometría simétrica te espera con los brazos abiertos.