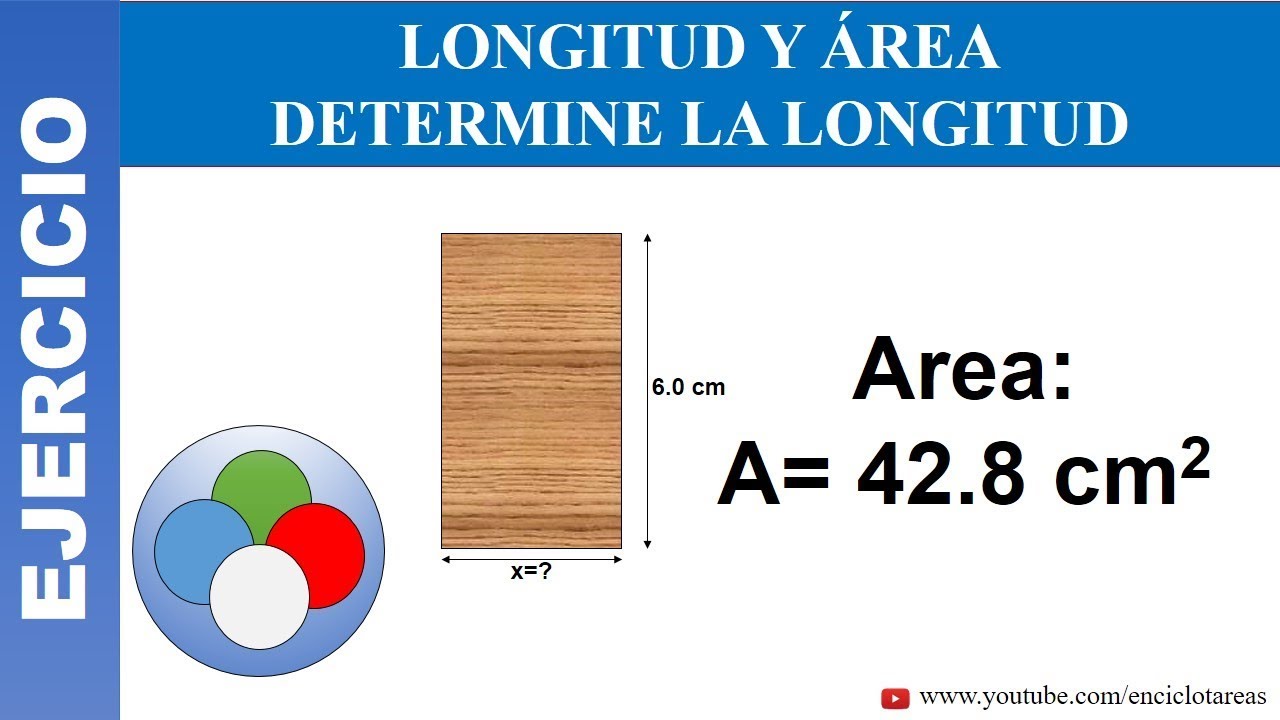
Cómo hallar la longitud de una figura
Descubre los trucos para calcular la longitud de cualquier forma geométrica
Calcular la longitud de una figura geométrica es esencial en diversas situaciones, ya sea en la vida diaria, en la ingeniería, la arquitectura o cualquier otro campo donde las dimensiones son fundamentales. En este artículo, exploraremos diferentes métodos para hallar la longitud de distintas figuras, desde segmentos rectilíneos simples hasta curvas más complejas.
Medición de longitudes rectilíneas
Para figuras con segmentos rectilíneos, como cuadrados, rectángulos o triángulos, el cálculo de la longitud es directo. Basta con sumar los lados de la figura para obtener el perímetro total.
Método de suma de lados
En un cuadrado con lados de longitud «a», el perímetro será 4a, mientras que en un triángulo con lados a, b y c, sumar los tres lados proporcionará la longitud total.
Aplicación práctica: El perímetro de una cerca rectangular
Imagina que estás diseñando una cerca rectangular para tu jardín. ¿Cómo calcularías la longitud total de la cerca para comprar la cantidad adecuada de material?
Longitudes en figuras circulares
En el caso de figuras circulares como círculos o elipses, el concepto de longitud se relaciona con la circunferencia. Calcular la circunferencia implica el uso de la fórmula específica para cada figura.
Fórmula de la circunferencia de un círculo
La circunferencia de un círculo se calcula multiplicando el radio por 2π. Siendo r el radio, la fórmula queda como: C = 2πr.
Aplicación práctica: La longitud de una pista de atletismo circular
¿Cuál sería la longitud total de una pista de atletismo si su radio es de 50 metros? ¿Y si quisieras saber cuántas vueltas darías para completar un kilómetro?
Longitudes en curvas complejas
En figuras con curvas complejas, como parábolas o espirales, determinar la longitud implica métodos más avanzados, como la integración. Este proceso puede ser desafiante pero es fundamental para aplicaciones en ingeniería y matemáticas.
Método de integración para curvas
La longitud de una curva se calcula mediante una integral definida, que requiere conocimientos de cálculo. Este método es preciso pero puede ser laborioso en curvas muy complejas.
Aplicación práctica: La longitud de un arco de parábola
Imagina que necesitas saber la longitud de un arco de parábola para diseñar una viga en una estructura arquitectónica. ¿Cómo abordarías este cálculo?
Calcular la longitud de una figura implica tanto desafíos intelectuales como gratificaciones al lograr precisión en las mediciones. Ya sea utilizando fórmulas simples o métodos avanzados, comprender cómo hallar la longitud es fundamental en diversos campos.
¿Cómo aplicar estos conceptos a situaciones cotidianas?
¿Qué otras aplicaciones prácticas puedes imaginar a partir de los métodos para hallar la longitud de una figura? ¡Atrévete a pensar más allá de las matemáticas y descubre cómo estas habilidades pueden ser útiles en tu vida diaria!