¿Alguna vez te has preguntado cómo determinar el ángulo entre dos rectas en un plano cartesiano? Calcular este ángulo puede ser un desafío, pero con los conceptos adecuados y un poco de práctica, ¡puedes dominarlo sin problemas!
Conceptos Básicos
Antes de sumergirnos en el cálculo del ángulo entre dos rectas, es crucial entender algunos conceptos básicos. En un plano cartesiano, una recta puede representarse mediante una ecuación de la forma y = mx + b, donde m es la pendiente de la recta y b es el término independiente. Dos rectas en el plano formarán un ángulo entre sí, y determinar este ángulo implica aplicar fórmulas trigonométricas y conocimientos de geometría.
Cálculo del Ángulo
Paso 1: Encontrar las Pendientes de las Rectas
El primer paso para calcular el ángulo entre dos rectas es determinar las pendientes de ambas rectas. Dado que el ángulo entre dos rectas es el ángulo formado por las dos pendientes, puedes usar la fórmula m = tan(θ) para obtener la pendiente m y luego el ángulo θ.
Paso 2: Calcular el Ángulo Utilizando la Fórmula
Una vez que tienes las pendientes de las dos rectas, puedes utilizar la fórmula del ángulo entre dos rectas en función de las pendientes. Esta fórmula se basa en las propiedades de las tangentes y arctangentes para encontrar el ángulo deseado.
Fórmula del Ángulo entre Dos Rectas:
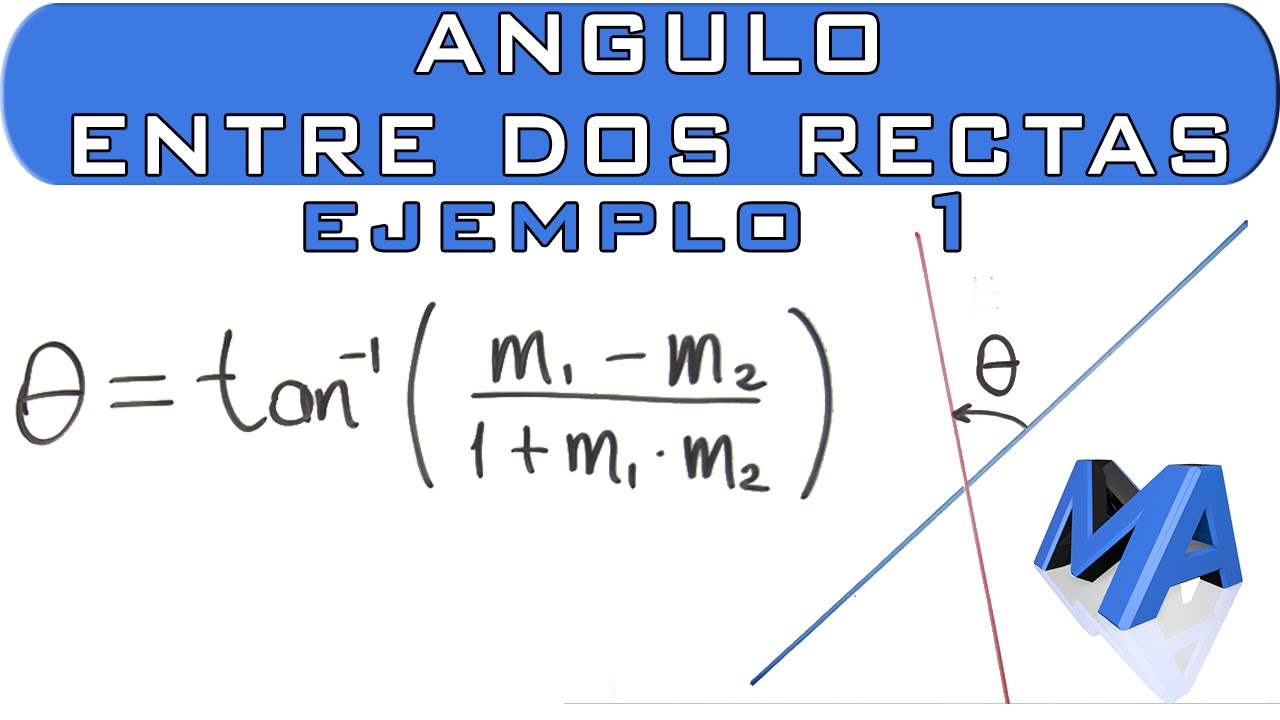
El ángulo entre dos rectas con pendientes m1 y m2 se puede calcular como:
θ = |arctan((m2 – m1) / (1 + m1 * m2))|
Ejemplo Práctico
Para comprender mejor este proceso, consideremos un ejemplo. Supongamos que tenemos dos rectas con pendientes m1 = 2 y m2 = -1. Aplicando la fórmula del ángulo entre dos rectas, sustituimos las pendientes en la fórmula y realizamos los cálculos para encontrar el valor del ángulo θ.
¿Por qué es importante calcular el ángulo entre dos rectas?
Calcular el ángulo entre dos rectas es crucial en geometría y trigonometría, ya que proporciona información sobre la orientación relativa de las rectas en un plano.
¿Qué sucede si las pendientes de las rectas son iguales?
Si las pendientes de las rectas son iguales, las rectas son paralelas, y el ángulo entre ellas es de 0 grados.
¿Se puede utilizar un enfoque geométrico para calcular el ángulo entre dos rectas?
Sí, también es posible calcular el ángulo entre dos rectas utilizando propiedades geométricas, como el producto escalar de los vectores direccionales de las rectas.
Con estos conceptos en mente, ahora estás listo para adentrarte en el fascinante mundo de la geometría analítica y el cálculo de ángulos entre rectas. ¡Explora, practica y disfruta del desafío de resolver problemas matemáticos intrigantes!