Explorando la Geometría: Angulos y Triángulos
En el fascinante mundo de la geometría, dos elementos fundamentales que capturan la esencia de las figuras planas son los ángulos y los triángulos. Estas formas geométricas son la base de muchos conceptos matemáticos y poseen propiedades únicas que nos permiten comprender mejor el espacio que nos rodea. En este artículo, nos sumergiremos en un viaje educativo que nos llevará a explorar la relación entre los ángulos y los triángulos, proporcionando un cuadro comparativo detallado para visualizar sus diferencias y similitudes.
Una Mirada Profunda a los Ángulos
Definición y Tipos de Ángulos
Comencemos nuestro viaje con los ángulos, los cuales son formados por dos rayos que comparten un punto en común, conocido como vértice. Existen varios tipos de ángulos, cada uno con características únicas que los distinguen:
Ángulo Agudo:
Un ángulo agudo es aquel cuya medida es menor a 90 grados. Imagina un triángulo rectángulo en el que uno de sus ángulos internos es agudo, como la punta de una flecha preparada para ser lanzada con precisión.
Ángulo Obtuso:
Contrario al ángulo agudo, un ángulo obtuso tiene una medida mayor a 90 grados pero menor a 180 grados. Puedes visualizarlo como la apertura de un libro que no se ha abierto por completo.
Ángulo Recto:
El ángulo recto es aquel cuya medida es exactamente de 90 grados, como la esquina de un cuadro perfectamente enmarcado.
Sumergiéndonos en el Mundo de los Triángulos
Definición y Clasificación de Triángulos
Ahora que hemos explorado los ángulos, es hora de adentrarnos en el intrigante mundo de los triángulos, figuras compuestas por tres segmentos de recta conectados entre sí. Los triángulos pueden clasificarse de diversas formas, siendo las más comunes:
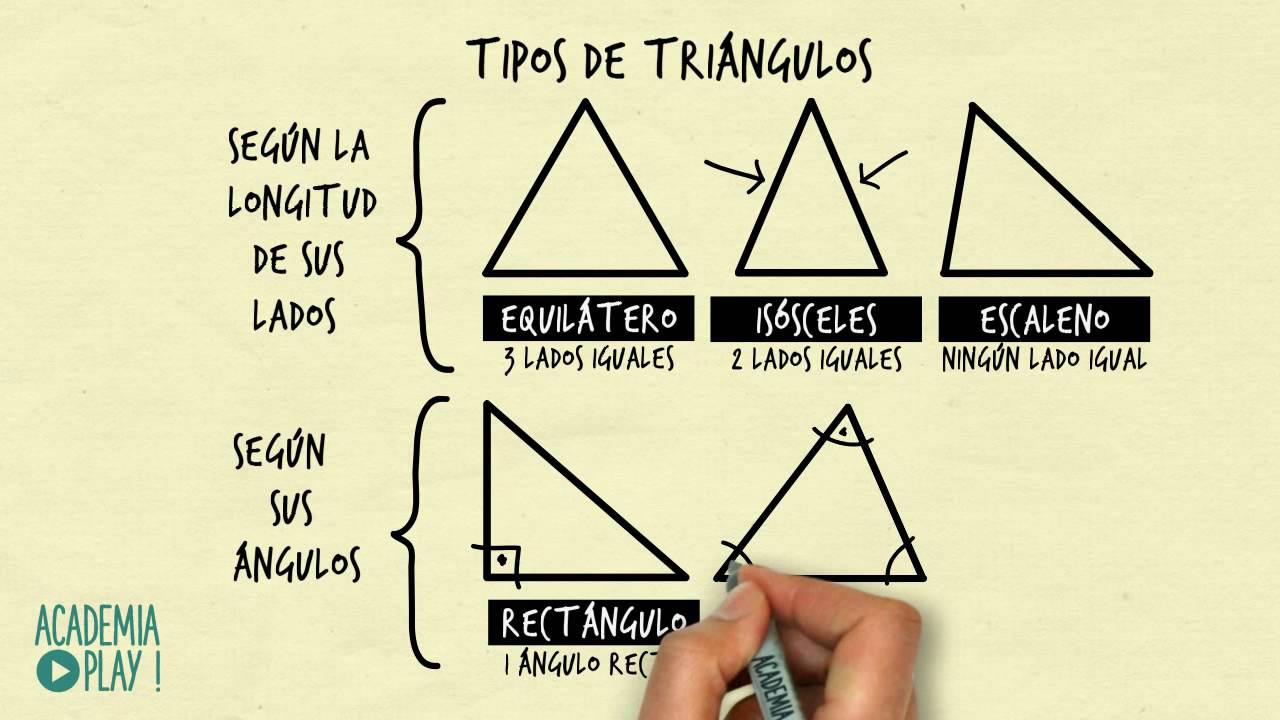
Triángulo Equilátero:
Un triángulo equilátero es aquel cuyos tres lados y tres ángulos internos son iguales, creando una simetría perfecta. Es como un trébol de tres hojas en el mundo geométrico.
Triángulo Isósceles:
En un triángulo isósceles, dos de sus lados son iguales en longitud, lo que provoca que dos de sus ángulos también lo sean. Este tipo de triángulo se asemeja a una cometa ondeando en el cielo.
Triángulo Escaleno:
Por último, el triángulo escaleno se caracteriza por tener todos sus lados y ángulos de longitudes y medidas diferentes, creando una asimetría visual única. Puedes imaginártelo como una flecha disparada en diferentes direcciones.
Comparando Ángulos y Triángulos: ¿Qué Tienen en Común?
A pesar de ser formas geométricas diferentes, los ángulos y los triángulos comparten ciertas características y propiedades que los hacen intrínsecamente relacionados en el campo de la geometría. Ambos conceptos son esenciales para comprender la estructura y las relaciones espaciales en el mundo que nos rodea.
Los Ángulos en los Triángulos:
En un triángulo, la suma de los ángulos internos siempre será igual a 180 grados. Esta propiedad demuestra la estrecha conexión entre los ángulos y los triángulos, ya que los ángulos individuales dentro de la figura se entrelazan para formar un total cohesionado.
Ángulos Externos de un Triángulo:
Los ángulos externos de un triángulo, aquellos formados por la extensión de un lado del triángulo, suman 360 grados. Esta característica revela la complejidad y la armonía geométrica presente en la interacción de los ángulos y los triángulos.
Explorando las Aplicaciones Prácticas de los Ángulos y los Triángulos
Ingeniería y Arquitectura:
En campos como la ingeniería y la arquitectura, el conocimiento profundo de los ángulos y los triángulos es crucial para diseñar estructuras sólidas y estables. Desde la construcción de puentes hasta la planificación de edificios, las propiedades geométricas de estas figuras son la base de la creatividad humana.
En el ámbito de la navegación y la cartografía, la comprensión de los ángulos y los triángulos es esencial para trazar rutas, determinar posiciones y cartografiar territorios. Los antiguos navegantes utilizaban astrolabios y sextantes, dispositivos basados en principios geométricos, para orientarse en alta mar.
En conclusión, los ángulos y los triángulos son elementos esenciales en el fascinante mundo de la geometría, ofreciendo un amplio abanico de posibilidades para explorar formas, dimensiones y relaciones espaciales. A medida que profundizamos en estas figuras geométricas, descubrimos un universo matemático repleto de simetrías, asimetrías y patrones intrigantes.
Preguntas Frecuentes sobre Ángulos y Triángulos:
¿Cuál es la relación entre los ángulos y los triángulos en geometría?
En geometría, los ángulos son componentes clave de los triángulos, ya que la suma de los ángulos internos de un triángulo siempre es igual a 180 grados.
¿Por qué es importante comprender la clasificación de los triángulos?
La clasificación de los triángulos nos permite identificar sus propiedades únicas y comprender mejor sus características individuales, lo que es fundamental en diversos campos como la geometría, la arquitectura y la ingeniería.