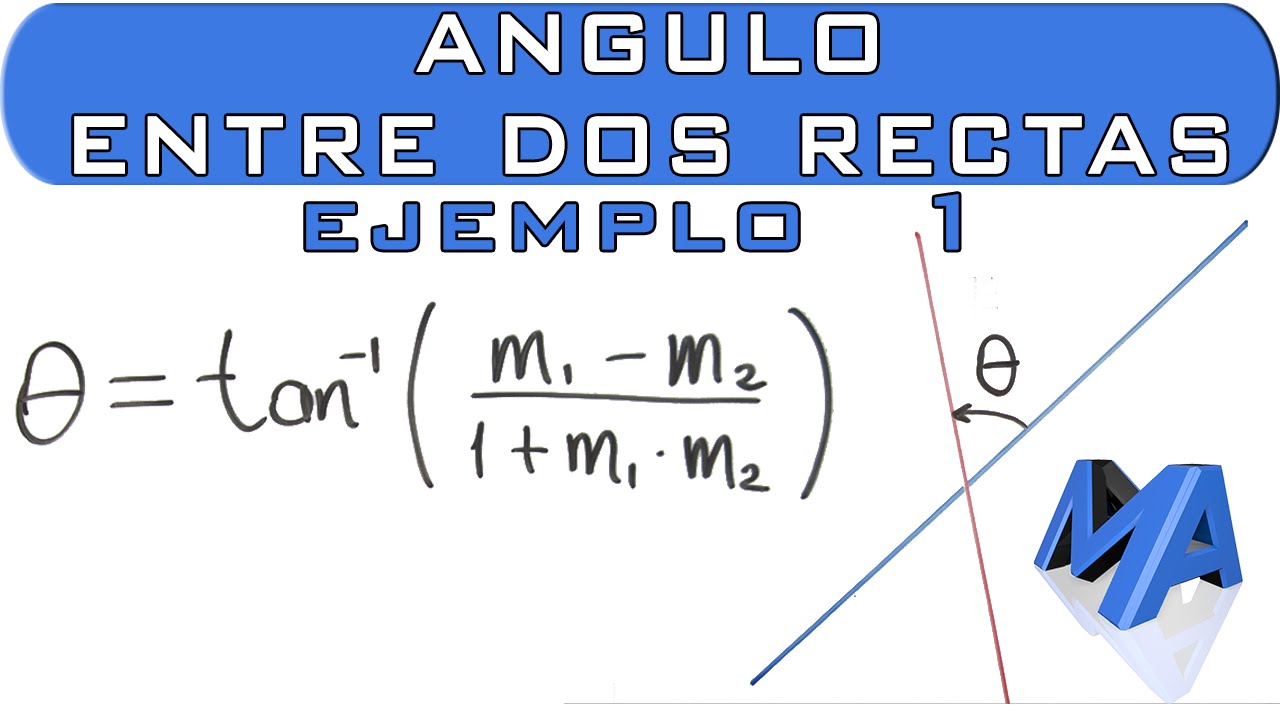
Los ángulos entre dos rectas son un concepto fundamental en geometría que nos permite comprender la relación entre dos líneas en un plano. Cuando dos rectas se intersecan, se forman distintos tipos de ángulos que pueden proporcionar información crucial sobre la disposición de las líneas y sus propiedades geométricas.
La importancia de comprender los ángulos entre dos rectas
Entender cómo se relacionan las rectas en un plano a través de los ángulos que forman es esencial en diversas ramas de las matemáticas y la física. Estos ángulos nos ayudan a determinar la perpendicularidad, paralelismo o cruce de las rectas, lo que tiene aplicaciones significativas en la resolución de problemas geométricos y en la interpretación de fenómenos físicos.
Ángulos formados por dos rectas transversales
Al trazar una tercera recta que corta a otras dos líneas, se crean diferentes tipos de ángulos. Los ángulos alternos internos, alternos externos, correspondientes y consecutivos son algunos de los ejemplos comunes de ángulos que se forman en este escenario. Cada tipo de ángulo tiene propiedades únicas que permiten analizar la disposición de las rectas en el plano.
Ángulos alternos internos y externos
Los ángulos alternos internos y externos son pares de ángulos que se forman en lados opuestos de la línea transversal cuando dos rectas se cortan. Estos ángulos son congruentes entre sí, lo que significa que tienen la misma medida. Esta propiedad es fundamental para demostrar la igualdad de ángulos en geometría.
Ángulos correspondientes
Los ángulos correspondientes son pares de ángulos que se encuentran en el mismo lado de la línea transversal, pero en distintas rectas. Si las dos líneas son paralelas, los ángulos correspondientes son congruentes. Esta relación es clave para identificar si las rectas son paralelas o no a través de la igualdad de ángulos.
Teorema de los ángulos internos y alternos
El teorema de los ángulos internos y alternos establece que, si dos rectas paralelas son cortadas por una tercera recta, entonces los pares de ángulos alternos internos son congruentes. Este teorema es esencial en la demostración de la igualdad de ángulos y en la determinación de propiedades de las rectas en un plano.
Ángulos adyacentes y suplementarios
Además de los ángulos formados por rectas transversales, también tenemos los ángulos adyacentes y suplementarios, que son importantes en el estudio de la geometría de las líneas. Los ángulos adyacentes comparten un lado y un vértice común, mientras que los ángulos suplementarios suman 180 grados.
Relación entre ángulos adyacentes y suplementarios
Los ángulos adyacentes pueden complementarse para formar ángulos suplementarios. Esta relación es útil para resolver ecuaciones de ángulos y comprender cómo se relacionan diferentes medidas angulares en un conjunto de líneas.
Propiedades de los ángulos adyacentes
Los ángulos adyacentes tienen la propiedad de compartir un lado y un vértice, lo que los hace útiles en la demostración de congruencia entre ángulos en distintas configuraciones geométricas. Esta propiedad es fundamental en la resolución de problemas geométricos avanzados.
Resolución de problemas con ángulos entre dos rectas
La comprensión de los ángulos entre dos rectas es esencial en la resolución de problemas geométricos y en la interpretación de fenómenos físicos que involucran líneas en un plano. La aplicabilidad de las propiedades angulares nos permite analizar situaciones complejas y encontrar soluciones de manera estructurada.
Aplicaciones prácticas de los ángulos entre dos rectas
Aplicar el conocimiento de los ángulos entre dos rectas en problemas de diseño arquitectónico, ingeniería civil o cálculos matemáticos avanzados es fundamental para garantizar la precisión y eficacia en los resultados. Las propiedades angulares orientan las decisiones profesionales en áreas que requieren un análisis detallado de las relaciones geométricas.
Importancia de la visualización geométrica en la comprensión de ángulos
La capacidad de visualizar las relaciones entre las rectas y los ángulos en un plano tridimensional amplifica la comprensión de conceptos como los ángulos entre dos rectas. La representación gráfica de las líneas y sus interacciones facilita el análisis y la interpretación de los problemas geométricos.
Utilización de herramientas tecnológicas en la visualización
Las herramientas tecnológicas, como software de geometría dinámica o programas de modelado tridimensional, son útiles para representar de manera interactiva las relaciones entre las rectas y los ángulos. Estas herramientas permiten explorar casos particulares y generalizar conceptos geométricos complejos.
Desarrollo de habilidades matemáticas a través de los ángulos entre dos rectas
El estudio de los ángulos entre dos rectas no solo ayuda a comprender las propiedades geométricas de las líneas, sino que también contribuye al desarrollo de habilidades matemáticas como la resolución de problemas, el razonamiento lógico y la visualización espacial. Estas competencias son valiosas en diversos campos académicos y profesionales.
Entrenamiento en la aplicación de conceptos geométricos
Practicar la resolución de problemas que involucren ángulos entre dos rectas fortalece la capacidad de aplicar conceptos matemáticos en situaciones concretas. La repetición de ejercicios ayuda a afianzar el conocimiento y a mejorar la habilidad para abordar desafíos geométricos de manera efectiva.
¿Cómo se identifican los ángulos entre dos rectas en un plano?
Para identificar los ángulos entre dos rectas en un plano, es necesario analizar la disposición de las líneas y utilizar las propiedades de los ángulos correspondientes, alternos internos y externos, entre otros. La visualización y la aplicación de teoremas geométricos son útiles en este proceso.
¿Por qué es importante comprender los ángulos entre dos rectas en la vida cotidiana?
La comprensión de los ángulos entre dos rectas tiene aplicaciones prácticas en diversas situaciones de la vida cotidiana, desde la construcción de edificaciones hasta la planificación urbana. Estos conceptos geométricos son fundamentales en el diseño y la resolución de problemas espaciales.
¿Cómo influyen los ángulos entre dos rectas en la toma de decisiones profesionales?
En entornos profesionales como la ingeniería, la arquitectura o la cartografía, los ángulos entre dos rectas influyen en la toma de decisiones relacionadas con la orientación de estructuras, la distribución de espacios y la resolución de problemas técnicos. La precisión en el análisis angular es crucial en estos campos.