Un tetraedro es un poliedro con cuatro caras triangulares. Calcular su volumen puede parecer complicado a simple vista, pero con los pasos correctos y un poco de comprensión geométrica, ¡puedes dominar este concepto de forma sencilla! En este artículo, te guiaré paso a paso en el proceso para encontrar el volumen de un tetraedro. ¡Vamos a sumergirnos en el fascinante mundo de la geometría!
Conoce los elementos clave de un tetraedro
Antes de abordar cómo hallar el volumen de un tetraedro, es fundamental comprender sus elementos clave. Un tetraedro consta de cuatro caras triangulares, seis aristas y cuatro vértices. Cada cara triangular se une a otras tres en un punto común, creando una figura tridimensional única. Al entender la estructura básica del tetraedro, estarás listo para realizar cálculos precisos de su volumen.
Fórmula para calcular el volumen de un tetraedro
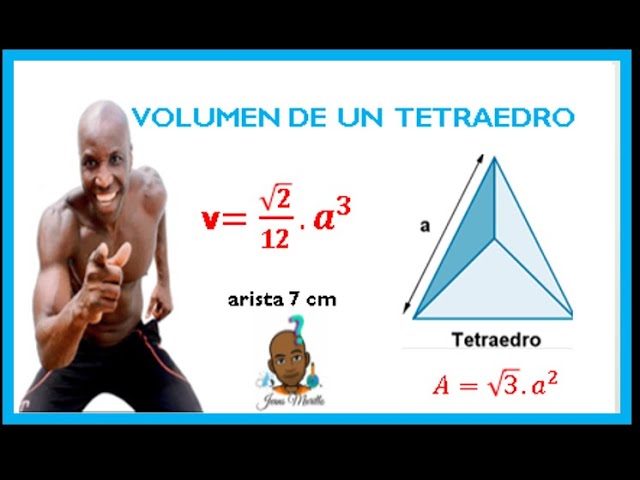
El volumen de un tetraedro se puede calcular utilizando una fórmula específica que involucra la longitud de sus aristas. La fórmula para el volumen de un tetraedro es:
V = (a³ * √2) / 12
Donde «V» representa el volumen, y «a» es la longitud de una arista del tetraedro. Esta fórmula te permitirá obtener el volumen de cualquier tetraedro dado su lado, lo que resulta útil en situaciones donde se requiere esta medida geométrica.
Determina la longitud de una arista
El primer paso para calcular el volumen de un tetraedro es determinar la longitud de una de sus aristas. Esta medida es crucial para aplicar la fórmula correctamente y obtener un resultado preciso. Puedes medir la arista si tienes el tetraedro físicamente presente o utilizar datos proporcionados en un problema geométrico.
Ejemplo práctico
Imaginemos que tenemos un tetraedro con una arista de 5 unidades de longitud. Para encontrar su volumen, sustituimos este valor en la fórmula previamente mencionada:
V = (5³ * √2) / 12
Al realizar los cálculos necesarios, obtendremos el volumen del tetraedro en unidades cúbicas. Este sencillo ejemplo ilustra cómo aplicar la fórmula en un escenario práctico, brindándote una comprensión más clara del proceso.
Aplica la fórmula del volumen
Una vez que tengas la longitud de una arista, es momento de aplicar la fórmula del volumen del tetraedro. Sustituye el valor de la arista en la fórmula y realiza las operaciones matemáticas necesarias para encontrar el volumen final. Recuerda mantener la precisión en tus cálculos para obtener resultados exactos.
Importancia del volumen en geometría
El volumen de un tetraedro es una medida crucial en geometría, ya que proporciona información sobre la capacidad de la figura y su ocupación en el espacio tridimensional. Comprender cómo hallar el volumen de un tetraedro te permitirá resolver problemas geométricos de manera eficiente y precisa.
Desafíos adicionales y aplicaciones
Una vez que domines el cálculo del volumen de un tetraedro, puedes enfrentarte a desafíos más complejos que involucren figuras tridimensionales. Explora diferentes formas geométricas y aplica tus conocimientos para encontrar sus volúmenes de manera sistemática. Además, considera cómo este concepto se aplica en contextos del mundo real, como la arquitectura y la ingeniería.
¿Es necesario conocer todas las aristas de un tetraedro para calcular su volumen?
No, basta con conocer la longitud de una arista para poder determinar el volumen del tetraedro utilizando la fórmula correspondiente. Es un proceso eficiente que simplifica los cálculos.
¿Se puede calcular el volumen de un tetraedro si solo se conocen las coordenadas de sus vértices?
Sí, es posible determinar el volumen de un tetraedro utilizando las coordenadas de sus vértices mediante cálculos que involucran determinantes y fórmulas específicas de geometría analítica. Este enfoque puede resultar más complejo pero igualmente válido.
En conclusión, el cálculo del volumen de un tetraedro es un proceso accesible con la comprensión adecuada de sus elementos y la aplicación de la fórmula correspondiente. Al dominar este concepto, ampliarás tus habilidades matemáticas y geométricas, abriendo nuevas puertas hacia la resolución de problemas en un contexto tridimensional. ¡Explora el mundo de la geometría con confianza y determinación!