El incentro de un triángulo es un concepto fundamental en geometría que nos permite encontrar el punto de intersección de las tres bisectrices internas de un triángulo. En este artículo, exploraremos paso a paso cómo identificar y calcular el incentro de un triángulo. Ya sea que seas un estudiante de matemáticas, un entusiasta de la geometría o simplemente alguien interesado en aprender algo nuevo, ¡este tema te fascinará!
¿Qué es el incentro de un triángulo?
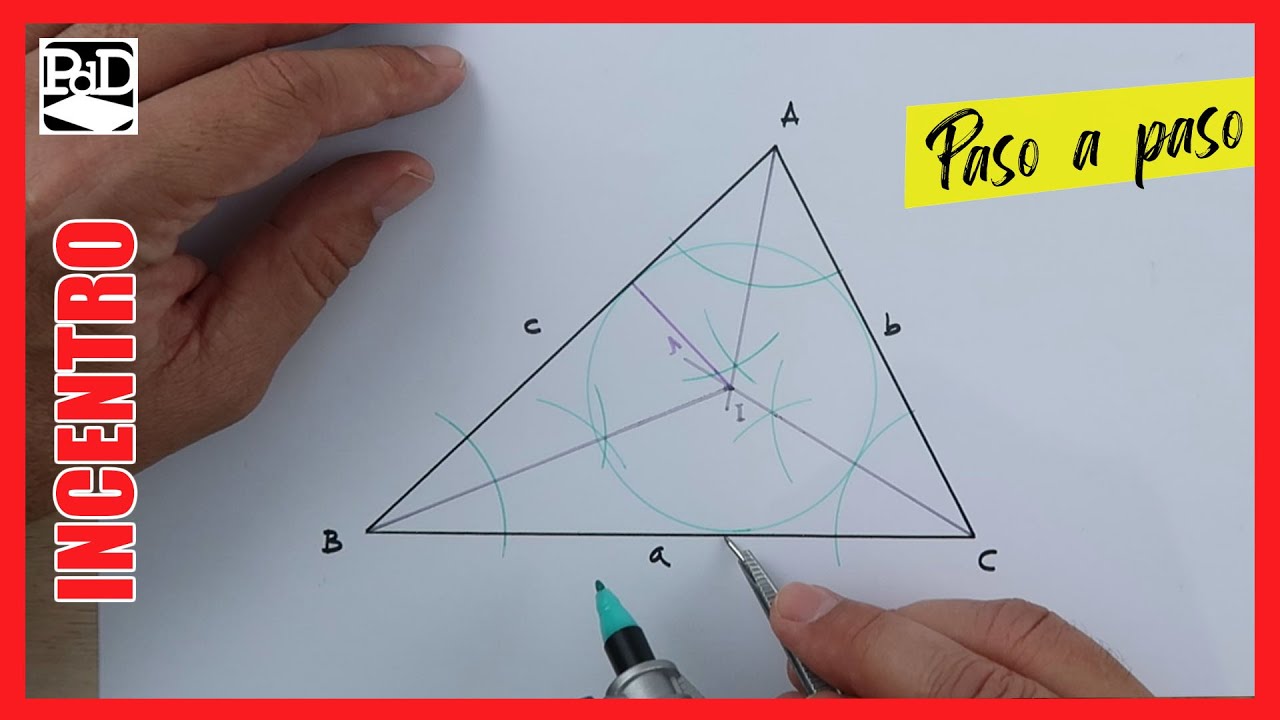
Antes de sumergirnos en el proceso de encontrar el incentro de un triángulo, es esencial comprender qué representa este punto. El incentro es el punto donde las bisectrices internas del triángulo se cruzan. En otras palabras, es el centro del círculo inscrito en el triángulo, que toca a los tres lados del triángulo. Este punto juega un papel crucial en diversas ramas de las matemáticas y la geometría debido a sus propiedades únicas.
Propiedades del incentro de un triángulo
El incentro de un triángulo equidista de los tres lados del triángulo, lo que significa que la distancia desde el incentro a cada lado del triángulo es la misma. Además, las líneas que conectan el incentro con los vértices del triángulo forman ángulos rectos. Estas propiedades hacen que el incentro sea un punto significativo en la geometría de un triángulo.
Paso 1: Identificar los lados y vértices del triángulo
Para encontrar el incentro de un triángulo, lo primero que debemos hacer es identificar los lados y vértices del triángulo en cuestión. Denotaremos los vértices como A, B y C, y sus lados opuestos respectivamente como a, b y c.
Paso 2: Encontrar las bisectrices internas del triángulo
Las bisectrices internas de un triángulo son las líneas que dividen los ángulos del triángulo en dos ángulos iguales. Para encontrar las bisectrices internas, podemos utilizar el concepto de las bisectrices exteriores y el incentro de un triángulo equilátero para guiar nuestro proceso.
Cálculo del incentro de un triángulo
Una vez que hemos identificado las bisectrices internas del triángulo, el siguiente paso es calcular las intersecciones de estas bisectrices para encontrar el incentro. Este proceso implica resolver un sistema de ecuaciones lineales para obtener las coordenadas del incentro.
Importancia del incentro en la geometría
El incentro no solo es un punto matemático intrigante, sino que también desempeña un papel crucial en la resolución de problemas geométricos avanzados. Desde la construcción de triángulos hasta la demostración de teoremas, el incentro proporciona una base sólida para el razonamiento geométrico.
Aplicaciones del incentro en la vida cotidiana
Aunque puede parecer abstracto, el concepto de incentro tiene aplicaciones prácticas en diversas situaciones cotidianas. La geometría del incentro se encuentra en el diseño arquitectónico, la ingeniería y la física, lo que demuestra su relevancia más allá del ámbito académico.
Curiosidades sobre el incentro de un triángulo
¿Sabías que el incentro de un triángulo siempre se encuentra dentro del triángulo, independientemente de su forma o tamaño? Esta propiedad fascinante ilustra la importancia y la consistencia del incentro en la geometría triangular.
Exploración adicional
La búsqueda del incentro de un triángulo es solo el comienzo de un viaje fascinante en el mundo de la geometría. Con cada nueva figura geométrica o concepto matemático que descubrimos, ampliamos nuestra comprensión del universo que nos rodea. ¡Sigue explorando y sorpréndete con las maravillas de las matemáticas!
¿El incentro de un triángulo siempre es un punto interior a la figura?
¿Cómo influye el incentro en el cálculo de áreas de triángulos y otras figuras geométricas?
¿Puede el incentro de un triángulo estar situado en uno de los vértices del triángulo?