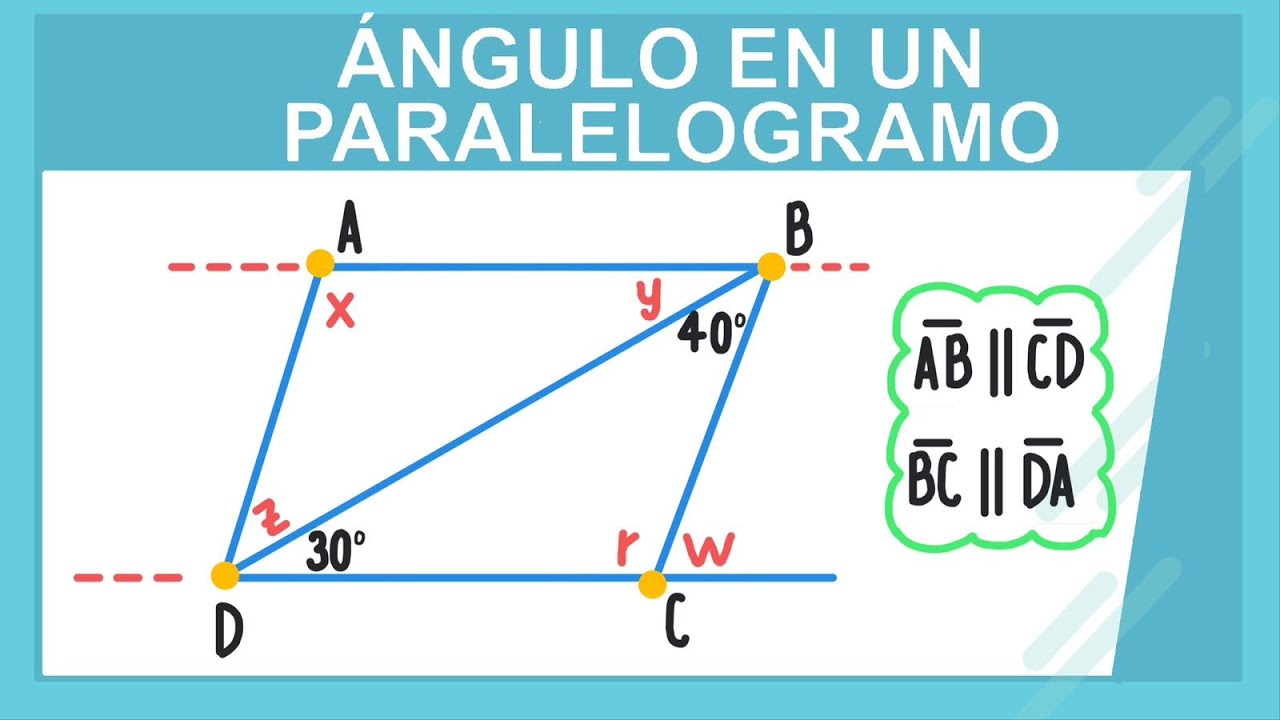
En el fascinante mundo de la geometría, los paralelogramos son figuras que poseen características únicas y propiedades matemáticas intrigantes. Uno de los aspectos más interesantes a explorar en un paralelogramo son las medidas de sus ángulos internos. Veamos de cerca este tema apasionante y descubramos más sobre cómo estos ángulos se relacionan entre sí en esta forma geométrica tan especial.
Explorando la relación entre los ángulos internos en un paralelogramo
¿Qué es un paralelogramo?
Para comprender plenamente las medidas de los ángulos internos en un paralelogramo, primero debemos definir qué es exactamente esta figura geométrica. Un paralelogramo es un cuadrilátero con lados opuestos paralelos entre sí, lo que implica que sus ángulos internos y lados presentan atributos específicos que los diferencian de otras formas.
Propiedades de los ángulos en un paralelogramo
Los paralelogramos poseen propiedades intrigantes en relación con sus ángulos internos. Los ángulos opuestos en un paralelogramo son iguales, y la suma de los ángulos adyacentes siempre equivale a 180 grados. Estas características geométricas únicas permiten realizar cálculos precisos y determinar las medidas de los ángulos internos con facilidad.
Analogía: Los ángulos en un paralelogramo como piezas de un rompecabezas
Imagina un rompecabezas donde cada ángulo en un paralelogramo es una pieza fundamental que encaja perfectamente con las demás para formar una figura completa y coherente. Al comprender cómo estos ángulos se relacionan entre sí, podemos resolver el rompecabezas geométrico del paralelogramo de manera efectiva.
Calculando ángulos internos en un paralelogramo
Una vez que hemos asimilado las propiedades fundamentales de los ángulos en un paralelogramo, surge la inevitable pregunta: ¿cómo podemos calcular las medidas exactas de estos ángulos internos en esta figura geométrica singular?
Métodos para determinar ángulos en un paralelogramo
Existen diversas estrategias para calcular los ángulos internos en un paralelogramo. Desde el uso de ecuaciones simples hasta la aplicación de teoremas matemáticos especializados, cada método nos brinda la oportunidad de desentrañar los misterios de la geometría del paralelogramo de manera precisa y rigurosa.
Ejemplo práctico: Resolviendo un problema de ángulos en un paralelogramo
Supongamos que se nos presenta un desafío que requiere determinar las medidas de los ángulos internos en un paralelogramo dado. Al aplicar nuestros conocimientos geométricos y habilidades matemáticas, podemos abordar este problema de manera sistemática y llegar a soluciones claras y concisas.
Interconexión de ángulos internos en un paralelogramo
Los ángulos internos en un paralelogramo no solo son elementos aislados, sino que están conectados de manera intrincada, formando un entramado geométrico fascinante que revela la elegancia y estructura subyacente en esta figura.
Visualización: Explorando la disposición de los ángulos internos en un paralelogramo
Al examinar la disposición de los ángulos internos en un paralelogramo mediante representaciones gráficas y diagramas intuitivos, podemos apreciar la armonía y simetría que subyacen en esta forma geométrica. Cada ángulo contribuye de manera significativa a la configuración general del paralelogramo, creando un conjunto equilibrado y coherente.
Aplicaciones prácticas: Utilidad de comprender los ángulos en un paralelogramo
La comprensión de las medidas de los ángulos internos en un paralelogramo no solo tiene relevancia en el ámbito académico, sino que también posee aplicaciones prácticas en diversos campos, como la arquitectura, la ingeniería y la cartografía. Estas aplicaciones reales resaltan la importancia de dominar los conceptos geométricos relacionados con los paralelogramos y sus ángulos internos.
¿Son los ángulos opuestos en un paralelogramo siempre iguales?
Sí, en un paralelogramo los ángulos opuestos son siempre iguales, lo que es una propiedad característica de esta figura geométrica.
¿Cómo puedo identificar un paralelogramo en un problema geométrico?
Para identificar un paralelogramo en un problema geométrico, es crucial buscar pistas como la presencia de lados paralelos y ángulos específicos que cumplan con las propiedades de esta figura.
¿Por qué es importante comprender los ángulos internos en un paralelogramo?
La comprensión de los ángulos internos en un paralelogramo es fundamental, ya que nos permite analizar la estructura y propiedades de esta figura geométrica, así como aplicar estos conocimientos en situaciones prácticas para resolver problemas matemáticos y de diseño.