¿Qué es la Geometría y cómo se relaciona con los ángulos?
Explorando los fundamentos de la Geometría
La Geometría es una rama de las matemáticas que se encarga del estudio de las formas, tamaños, posiciones y dimensiones de objetos y figuras en el espacio. Desde tiempos antiguos, los matemáticos han explorado las propiedades de las figuras geométricas para comprender el mundo que nos rodea. La Geometría no solo es una disciplina teórica, sino que también tiene aplicaciones prácticas en diversos campos, como la arquitectura, la ingeniería, la física y la computación.
La importancia de los ángulos en Geometría
Los ángulos son una parte fundamental de la Geometría, ya que nos permiten medir la separación entre dos líneas, rayos o segmentos de recta que se encuentran en un punto común, también conocido como vértice. Comprender los ángulos es esencial para analizar la disposición y orientación de las figuras geométricas, así como para resolver problemas geométricos en diferentes contextos. En este artículo, exploraremos diversos conceptos relacionados con la Geometría y los ángulos, desde sus definiciones básicas hasta aplicaciones prácticas en la vida cotidiana.
Conceptos Básicos de Geometría
Puntos, Líneas y Planos
En Geometría, un punto es una ubicación en el espacio que no tiene dimensiones. Al unir dos puntos, se forma una línea, que se extiende en ambas direcciones de forma infinita. Varios puntos forman un plano, que es una superficie plana sin grosor que se extiende indefinidamente. Estos elementos básicos son fundamentales para construir figuras geométricas más complejas.
Figuras Geométricas
Las figuras geométricas son formas bidimensionales o tridimensionales que pueden clasificarse en diferentes tipos, como triángulos, cuadrados, círculos, cubos, esferas, entre otros. Cada figura tiene propiedades y características únicas que permiten identificarlas y analizar su comportamiento en diferentes situaciones.
Tipos de Ángulos
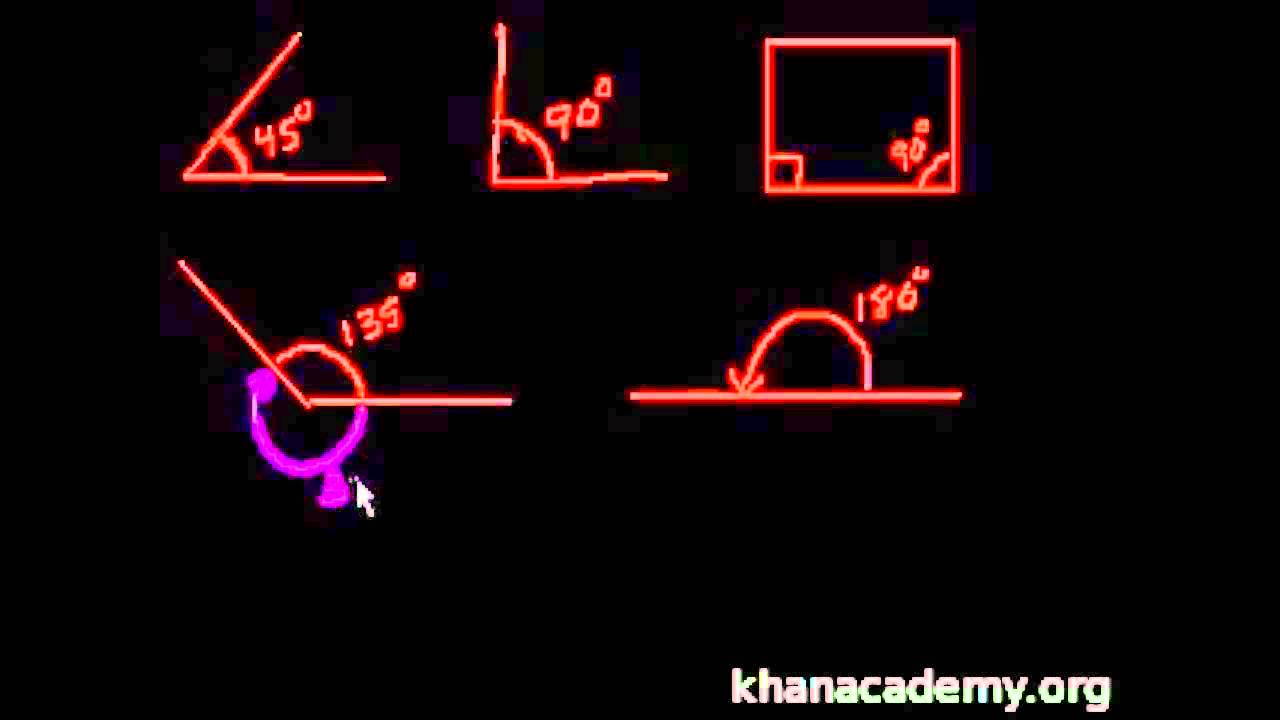
Ángulo Agudo
Un ángulo agudo es aquel cuya medida es mayor a 0° y menor a 90°. Visualmente, un ángulo agudo se parece a la esquina de una hoja de papel. Estos ángulos suelen encontrarse en diferentes configuraciones geométricas y son fundamentales para comprender la relación espacial entre diferentes elementos.
Ángulo Recto
Un ángulo recto tiene una medida de exactamente 90°, lo que significa que forma una esquina perfecta. Los ángulos rectos son comunes en la Geometría y en aplicaciones cotidianas, como la arquitectura y la carpintería, donde la precisión en ángulos rectos es crucial para la construcción de estructuras estables.
Ángulo Obtuso
Un ángulo obtuso es aquel cuya medida es mayor a 90° y menor a 180°. Estos ángulos son más abiertos que un ángulo recto y se encuentran en diversas situaciones geométricas, como en polígonos con lados extendidos. Comprender los ángulos obtusos es importante para resolver problemas de distribución espacial.
Propiedades de los Ángulos
Suma de Ángulos
En Geometría, la suma de los ángulos en un triángulo siempre es igual a 180°. Esta propiedad es conocida como la suma de ángulos internos de un triángulo y es fundamental para resolver problemas triangulares y demostrar teoremas geométricos.
7. Ángulos Complementarios y Suplementarios
Los ángulos complementarios son aquellos que, al sumarse, resultan en un ángulo recto de 90°. Por otro lado, los ángulos suplementarios son aquellos cuya suma es de 180°, formando un ángulo llano. Estas relaciones entre ángulos son útiles para realizar cálculos y resolver ecuaciones geométricas.
Aplicaciones de la Geometría y los Ángulos
Diseño Arquitectónico
En el campo de la arquitectura, la Geometría y los ángulos son fundamentales para el diseño de edificios, estructuras y espacios interiores. Los arquitectos utilizan conceptos geométricos para crear planos, distribuir espacios de manera eficiente y garantizar la estabilidad de las construcciones.
Tecnología y Gráficos por Computadora
En la industria de la tecnología, la Geometría desempeña un papel crucial en el desarrollo de gráficos por computadora, videojuegos y animaciones 3D. Los programadores y diseñadores utilizan principios geométricos para modelar objetos tridimensionales, crear efectos visuales realistas y simular entornos virtuales.
Desafíos en la Comprensión de la Geometría y los Ángulos
Visualización Espacial
Algunas personas pueden enfrentar dificultades al visualizar objetos en el espacio tridimensional, lo que puede dificultar la comprensión de conceptos geométricos avanzados. Prácticas como la utilización de modelos físicos o software de modelado 3D pueden ayudar a mejorar la habilidad de visualización espacial.
Abstracción Matemática
La Geometría implica un grado de abstracción matemática que puede resultar desafiante para aquellos que prefieren enfoques más concretos en el aprendizaje. Sin embargo, la práctica constante y la aplicación de conceptos a situaciones reales pueden facilitar la comprensión de la Geometría y los ángulos.
La Belleza de la Geometría y los Ángulos en la Naturaleza
Patrones Geométricos
La naturaleza está repleta de patrones geométricos fascinantes, desde las espirales en las conchas marinas hasta las estructuras hexagonales de los panales de abejas. Estos patrones reflejan la aplicabilidad universal de la Geometría y cómo el mundo natural sigue principios matemáticos intrincados en su diseño.
Simetría y Armonía
La simetría es un principio geométrico que se encuentra en la mayoría de los elementos naturales, como las alas de una mariposa o la estructura de una flor. La armonía y equilibrio visual que proporciona la simetría reflejan la belleza matemática subyacente en la naturaleza y resaltan la importancia de los ángulos en la creación de formas simétricas.
¿Por qué es importante entender los ángulos en Geometría?
Comprender los ángulos en Geometría es esencial, ya que nos permite analizar relaciones espaciales, resolver problemas matemáticos y aplicar conceptos geométricos en diferentes situaciones de la vida diaria. Los ángulos son como las piezas fundamentales de un rompecabezas geométrico que nos ayudan a construir una imagen completa de nuestro entorno.
¿Cómo puedo mejorar mi comprensión de la Geometría y los ángulos?
Para mejorar tu comprensión de la Geometría y los ángulos, te recomiendo practicar con ejercicios de dibujo, resolver problemas geométricos, utilizar herramientas de visualización espacial y explorar aplicaciones prácticas de la Geometría en campos como la arquitectura, la ingeniería y la decoración. La perseverancia y la exploración activa de conceptos te llevarán a descubrir la belleza y versatilidad de la Geometría en el mundo que nos rodea.