Explorando la Geometría del Triángulo
¡Bienvenidos al fascinante mundo de la geometría! En este artículo, nos sumergiremos en los misterios y maravillas que rodean a los triángulos, una de las figuras más básicas pero fundamentales en el campo de las matemáticas. Desde los sorprendentes vértices hasta las enigmáticas aristas, descubriremos juntos los secretos que hacen que estos polígonos sean tan intrigantes y relevantes en diferentes áreas de nuestras vidas. ¿Estás listo para embarcarte en este viaje de descubrimiento? ¡Vamos allá!
Los Vértices: Puntos de Encuentro
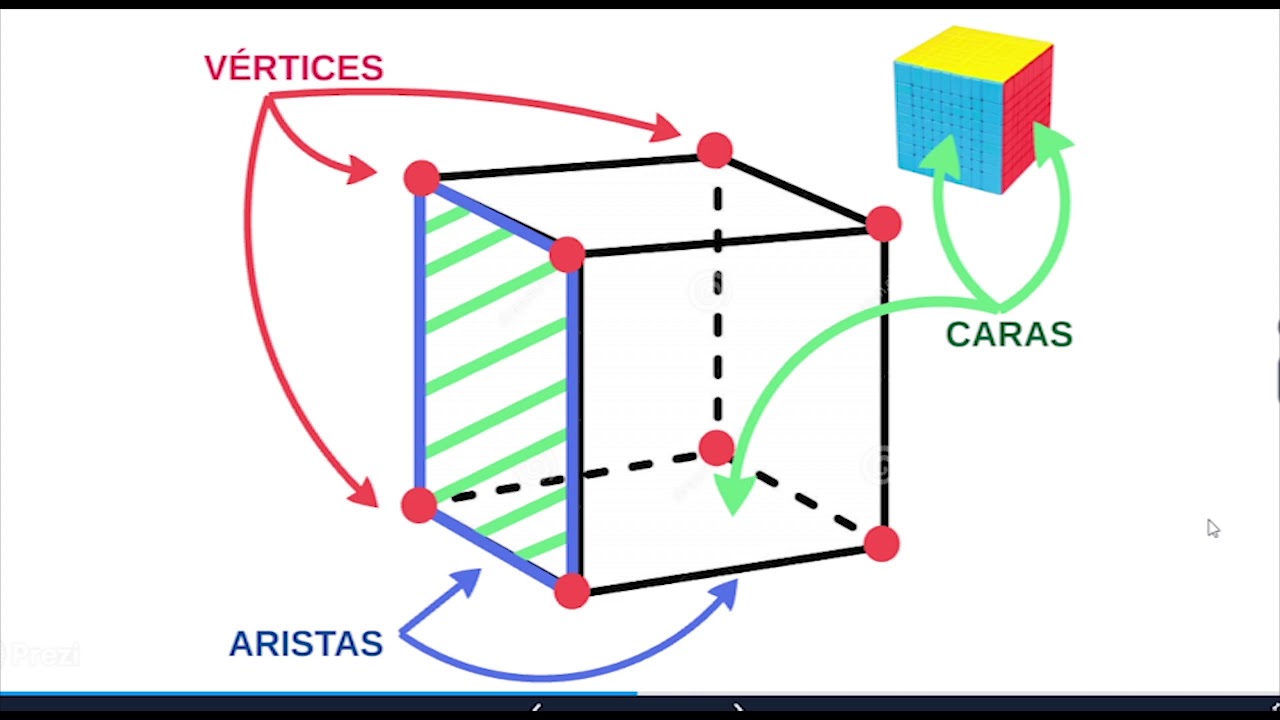
Comencemos nuestra exploración por uno de los elementos más distintivos de cualquier triángulo: los vértices. Los vértices son los puntos donde se encuentran dos o más segmentos de recta, también conocidos como aristas, que forman las distintas esquinas de la figura geométrica. En un triángulo, siempre encontraremos tres vértices, cada uno representado por un par de coordenadas en un plano cartesiano. Estos puntos de encuentro son cruciales para definir la forma y las propiedades del triángulo, ya que determinan ángulos y longitudes que nos ayudan a comprender mejor su estructura. Imagina los vértices como los hitos que guían nuestro camino a través de las geometrías del espacio. Cada vértice es único en su posición y contribuye de manera significativa a la identidad y clasificación del triángulo en cuestión.
Los Tipos de Vértices
Los vértices de un triángulo pueden ser clasificados en función de sus ángulos internos y sus lados. Según la medida de sus ángulos, los triángulos pueden ser clasificados como equiláteros, isósceles o escalenos. En un triángulo equilátero, todos los ángulos y lados son iguales, lo que le otorga una simetría perfecta. En contraste, un triángulo isósceles tiene al menos dos ángulos y lados iguales, creando una forma más asimétrica pero aún equilibrada. Por último, un triángulo escaleno posee todos sus ángulos y lados distintos, lo que resulta en una figura más irregular pero igualmente fascinante. Cada tipo de triángulo tiene sus propias características únicas que los hacen especiales y atractivos para los amantes de la geometría. ¿Cuál es tu tipo de triángulo favorito?
Las Aristas: Conexiones Invisibles
Ahora que hemos explorado los vértices, es momento de adentrarnos en un aspecto igualmente relevante de los triángulos: las aristas. Las aristas son los segmentos de recta que conectan los vértices entre sí, creando una red de interconexiones invisibles que definen la estructura global del triángulo. Cada arista representa una relación directa entre dos vértices, estableciendo así las distancias y relaciones espaciales dentro de la figura. Estas líneas de conexión nos permiten visualizar y analizar las propiedades geométricas del triángulo, desde sus longitudes y ángulos hasta sus posibles simetrías y transformaciones. Considera las aristas como los hilos invisibles que tejen la tela de la geometría, creando un patrón único y significativo que revela la belleza inherente de esta disciplina matemática.
La Importancia de las Aristas
Las aristas de un triángulo desempeñan un papel crucial en la identificación y clasificación de la figura. A través de la comparación de las longitudes de las aristas y los ángulos formados por ellas, los matemáticos y geometras pueden determinar las características específicas de un triángulo, como su tipo, área y perímetro. Además, las aristas también son fundamentales para el estudio de las propiedades trigonométricas y las transformaciones geométricas que se pueden aplicar a estos polígonos. Al comprender a fondo las aristas de un triángulo, podemos desvelar los enigmas que rodean su configuración y estructura, permitiéndonos apreciar aún más la elegancia y complejidad de estas formas geométricas.
Explorando las Propiedades y Aplicaciones de los Triángulos
Las Propiedades Únicas de los Triángulos
Los triángulos son figuras geométricas fascinantes que poseen una amplia gama de propiedades únicas y sorprendentes. Desde la suma de sus ángulos internos hasta la relación entre sus lados, los triángulos desafían nuestra percepción del espacio y la forma, ofreciéndonos un sinfín de posibilidades para la exploración matemática. Una de las propiedades más intrigantes de los triángulos es la famosa desigualdad triangular, que establece que la suma de las longitudes de dos lados de un triángulo siempre es mayor que la longitud del tercer lado. Esta propiedad es fundamental para la clasificación de triángulos y nos brinda información valiosa sobre las relaciones entre sus elementos constituyentes. ¿Qué otras propiedades de los triángulos te parecen más interesantes?
Las Aplicaciones Prácticas de los Triángulos
Aparte de su importancia en el ámbito matemático y geométrico, los triángulos también tienen numerosas aplicaciones prácticas en diversos campos de la ciencia y la ingeniería. Por ejemplo, en la trigonometría, los triángulos son fundamentales para el cálculo de distancias y ángulos en problemas de navegación, topografía y astronomía. Además, en la arquitectura y el diseño, los triángulos se utilizan para crear estructuras estables y equilibradas que resisten fuerzas externas y proporcionan soporte estructural. Incluso en la naturaleza, encontramos ejemplos de triángulos en la forma de cristales, hojas y formaciones geológicas que siguen patrones geométricos precisos. ¿Puedes pensar en otras aplicaciones prácticas de los triángulos en nuestro entorno cotidiano?
Resolviendo Enigmas Geométricos con Triángulos
Los Teoremas Clásicos de los Triángulos
Uno de los pilares de la geometría euclidiana son los teoremas y proposiciones relacionados con los triángulos, que han sido estudiados y demostrados a lo largo de los siglos por matemáticos de renombre. Algunos de los teoremas clásicos más conocidos son el Teorema de Pitágoras, que establece la relación fundamental entre los lados de un triángulo rectángulo, y el Teorema de Tales, que describe la proporcionalidad en triángulos semejantes. Estos teoremas, junto con muchos otros, nos brindan herramientas poderosas para resolver problemas geométricos complejos y profundizar en la belleza y simplicidad de las formas triangulares. ¿Cuál es tu teorema geométrico favorito y por qué?
La Geometría Analítica: Triángulos en el Plano Cartesiano
Otro enfoque fascinante para estudiar triángulos es a través de la geometría analítica, que combina conceptos geométricos con técnicas algebraicas para analizar las propiedades y relaciones en el plano cartesiano. Al representar los vértices de un triángulo como pares de coordenadas (x, y), podemos aplicar fórmulas y ecuaciones para calcular longitudes, áreas y otros parámetros geométricos de manera precisa. Este enfoque nos permite abordar problemas complejos de geometría con herramientas matemáticas avanzadas, ampliando así nuestra comprensión y apreciación de la geometría en un contexto más abstracto y analítico. ¿Cómo crees que la geometría analítica ha enriquecido nuestra comprensión de los triángulos y otras figuras geométricas?
Explorando los Triángulos desde una Perspectiva Creativa
La Belleza Estética de los Triángulos
Más allá de sus propiedades matemáticas y aplicaciones prácticas, los triángulos poseen una belleza estética que ha cautivado a artistas, diseñadores y arquitectos a lo largo de la historia. La simetría y la simplicidad de la forma triangular la hacen especialmente atractiva para la creación de obras visuales y estructuras impresionantes que despiertan nuestra imaginación y sensibilidad estética. Desde las pirámides de Egipto hasta las modernas obras de arte geométrico, los triángulos han sido una fuente de inspiración infinita para la creatividad humana, demostrando que las matemáticas y el arte están intrínsecamente entrelazados en la exploración de la forma y el espacio. ¿Cuál es tu creación artística favorita que involucra triángulos?
La Geometría Fractal: Triángulos en la Naturaleza
Un fenómeno fascinante que involucra triángulos es la geometría fractal, que se manifiesta en patrones repetitivos y autosimilares en la naturaleza. Desde los copos de nieve hasta las ramificaciones de los árboles, los triángulos se encuentran en una variedad de formas naturales que siguen principios fractales en su estructura y diseño. La geometría fractal nos invita a explorar la interconexión entre las matemáticas y la naturaleza, revelando la presencia de patrones geométricos subyacentes que dan forma a nuestro mundo de una manera sorprendentemente armoniosa y compleja. ¿Puedes identificar algún ejemplo de geometría fractal basada en triángulos en tu entorno?
Preguntas Frecuentes sobre Vértices y Aristas en un Triángulo
¿Cuál es la diferencia entre un vértice y una arista en un triángulo?
Los vértices son los puntos de encuentro de los segmentos de recta en un triángulo, mientras que las aristas son los segmentos que conectan estos vértices entre sí. Mientras que los vértices definen las esquinas del triángulo, las aristas establecen las conexiones entre ellos, creando así la estructura global de la figura geométrica.
¿Por qué son importantes los vértices y aristas en la geometría de un triángulo?
Los vértices y aristas son fundamentales para la identificación, clasificación y estudio de un triángulo, ya que nos permiten comprender su forma, propiedades y relaciones geométricas. A través de los vértices y aristas, podemos analizar los ángulos, lados y simetrías de un triángulo, desvelando así los secretos y enigmas que lo rodean.
¿Cómo se pueden aplicar los conceptos de vértices y aristas de un triángulo en la vida cotidiana?
Los conceptos de vértices y aristas de un triángulo tienen numerosas aplicaciones prácticas en campos como la arquitectura, la ingeniería, la navegación y la topografía. Al comprender la geometría de los triángulos, podemos diseñar estructuras estables, calcular distancias y ángulos, y resolver problemas espaciales de manera eficiente y precisa en nuestro entorno cotidiano.
¿Qué otros aspectos de la geometría de un triángulo se pueden explorar más allá de los vértices y aristas?
Además de los vértices y aristas, los triángulos presentan una variedad de propiedades y teoremas intrigantes que abarcan desde la suma de sus ángulos internos hasta las relaciones trigonométricas y proporciones de sus lados. Explorar temas como la semejanza, la congruencia y las transformaciones geométricas nos permite profundizar en la riqueza y diversidad de los triángulos en el mundo de las matemáticas y la geometría.
¡Espero que hayas disfrutado este viaje de descubrimiento a través de los vértices y aristas en un triángulo! La geometría es un mundo fascinante lleno de sorpresas y maravillas que nos invita a explorar y aprender cada día. ¿Qué aspecto de la geometría del triángulo te ha parecido más interesante o intrigante? ¡Comparte tus pensamientos y descubrimientos con nosotros!