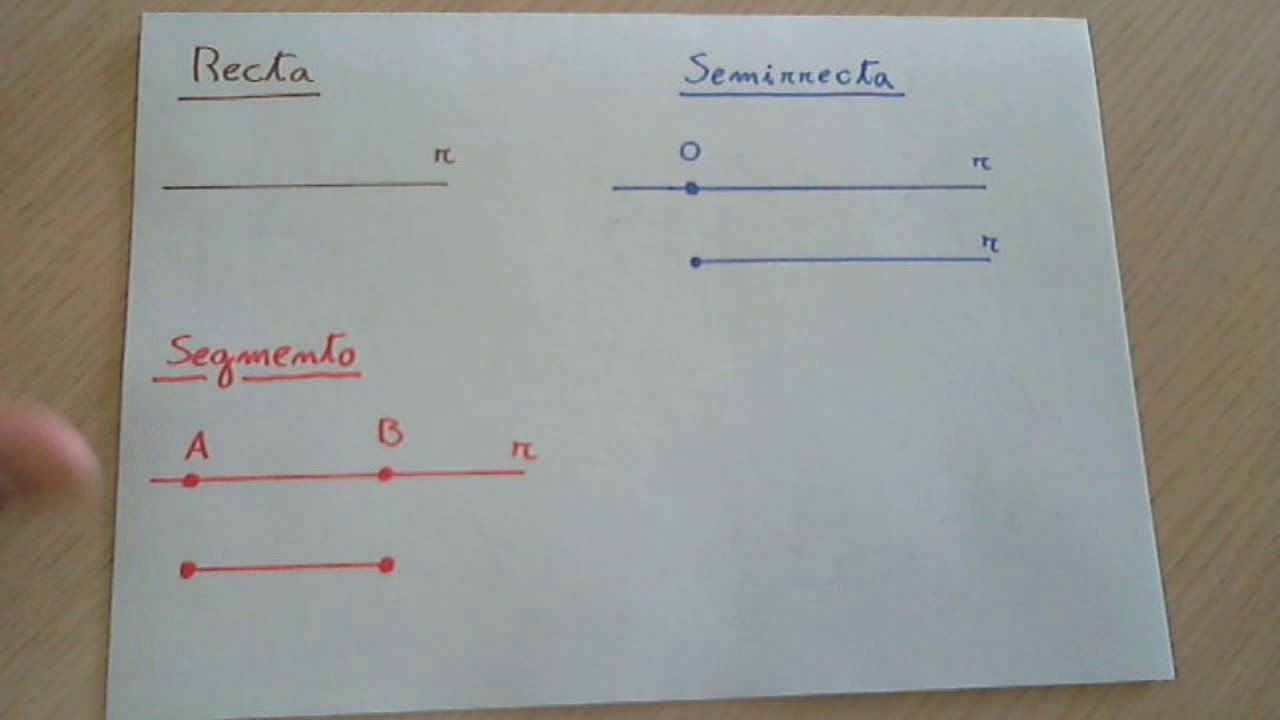
Una semirrecta es un término geométrico que se utiliza comúnmente en matemáticas para describir una línea que tiene un punto final y se extiende infinitamente en una dirección. Sin embargo, en algunos contextos, este concepto puede tener otro nombre que puede ser menos conocido para muchos. Exploraremos este concepto en profundidad y descubriremos ese otro término que se refiere a lo que comúnmente conocemos como semirrecta.
Descubriendo la nomenclatura alternativa
Cuando hablamos de semirrectas, es fundamental comprender que estas entidades geométricas son parte integral de la geometría y juegan un papel crucial en diversas aplicaciones matemáticas y en la resolución de problemas geométricos. Pero, ¿qué sucede cuando nos referimos a una semirrecta con un término distinto? ¿Cuál es esa denominación alternativa que puede sorprender a muchos? Sigue leyendo para descubrirlo.
La semirrecta en su esencia geométrica
Antes de adentrarnos en la designación alternativa de la semirrecta, es esencial comprender en qué consiste este concepto en su forma más básica. Una semirrecta se define como una línea que tiene un punto de origen y se extiende indefinidamente en una dirección especificada. Esta característica la distingue de una línea recta, que se extiende en ambas direcciones sin límites.
Características clave de una semirrecta
Para visualizar mejor una semirrecta, imagínala como una flecha que se origina en un punto y apunta en una sola dirección sin fin. Esta peculiaridad geométrica es fundamental en geometría analítica y en diversas ramas de las matemáticas, aportando la noción de dirección y extensión infinita en un solo sentido.
Uso de semirrectas en geometría
En geometría, las semirrectas se emplean para trazar ángulos, determinar posiciones relativas entre líneas y puntos, así como para representar direcciones en un plano cartesiano. Su naturaleza unidireccional facilita la resolución de problemas geométricos y la representación visual de líneas en el espacio euclidiano.
El término menos conocido para una semirrecta
Tras explorar en detalle la definición y el papel de las semirrectas en geometría, es momento de revelar el término menos conocido pero igualmente válido para referirse a estas entidades geométricas. El concepto que se oculta detrás de la semirrecta y que puede resultar desconocido para muchos es…
El «semiplano abierto»
El término «semiplano abierto» se utiliza en algunos contextos geométricos como una alternativa a la noción de semirrecta. Si bien ambas denominaciones hacen referencia a la misma entidad geométrica, el uso de «semiplano abierto» puede variar según el enfoque matemático o la preferencia del autor.
Diferencias sutiles pero significativas
Aunque el concepto de semirrecta y semiplano abierto son equivalentes en muchos aspectos, algunas diferencias sutiles pueden surgir en la interpretación de estas entidades geométricas. Es importante comprender que estas designaciones son herramientas conceptuales que nos ayudan a visualizar y trabajar con líneas en el plano cartesiano y el espacio euclidiano.
Aplicaciones avanzadas de semirrectas o semiplanos abiertos
En contextos más avanzados de geometría y matemáticas, el uso de semirrectas o semiplanos abiertos adquiere mayor relevancia en la modelización de fenómenos físicos, en la resolución de problemas de optimización y en el análisis de estructuras geométricas complejas. Estas entidades geométricas sirven como cimientos para desarrollar teoremas y resultados fundamentales en diversas ramas de las matemáticas.
Profundizando en la equivalencia de conceptos
Para comprender mejor la relación entre una semirrecta y un semiplano abierto, es crucial analizar cómo estos conceptos se interrelacionan en el contexto geométrico y matemático. Al explorar esta equivalencia, ampliamos nuestra perspectiva sobre la versatilidad de estos términos y su aplicabilidad en diferentes situaciones problemáticas.
Conexiones entre semirrectas y semiplanos abiertos
Las semirrectas y los semiplanos abiertos comparten similitudes en su definición y funcionamiento, lo que permite establecer conexiones significativas entre ambos conceptos. Desde la representación gráfica hasta su aplicación en cálculos vectoriales, la equivalencia entre estas entidades geométricas enriquece nuestro entendimiento de la geometría moderna.
Uso en geometría analítica
En el ámbito de la geometría analítica, tanto las semirrectas como los semiplanos abiertos se convierten en herramientas indispensables para trazar vectores, calcular intersecciones y definir regiones del plano cartesiano. Su flexibilidad y precisión los convierten en elementos fundamentales en la resolución de problemas geométricos complejos.
Explorando la dualidad conceptual
Al sumergirnos en la dualidad conceptual entre las semirrectas y los semiplanos abiertos, nos adentramos en un mundo de posibilidades matemáticas y geométricas que desafían nuestra percepción tradicional de las líneas y los planos. Esta dualidad nos invita a reflexionar sobre la riqueza conceptual que subyace a estos términos aparentemente simples pero profundamente significativos.
Consideraciones finales
En conclusión, aunque el término «semirrecta» es ampliamente conocido y utilizado en el ámbito de la geometría, el concepto de «semiplano abierto» ofrece una perspectiva alternativa y enriquecedora sobre esta entidad geométrica. Ya sea que nos refiramos a una semirrecta o a un semiplano abierto, la esencia geométrica subyacente sigue siendo la misma, brindándonos herramientas poderosas para explorar y comprender el mundo matemático que nos rodea.
¿Cuál es la diferencia entre una semirrecta y un semiplano abierto?
La diferencia principal radica en la nomenclatura y la interpretación contextual, ya que ambos conceptos representan una línea unidireccional en el plano.
¿En qué contextos se prefiere utilizar el término «semiplano abierto» en lugar de «semirrecta»?
El término «semiplano abierto» suele ser más común en contextos de geometría analítica avanzada y en teoría de conjuntos, donde se enfatiza la noción topológica de apertura y cierre en conjuntos geométricos.
¡Esperamos que este artículo te haya brindado una nueva perspectiva sobre las semirrectas y los semiplanos abiertos en el fascinante mundo de la geometría matemática!