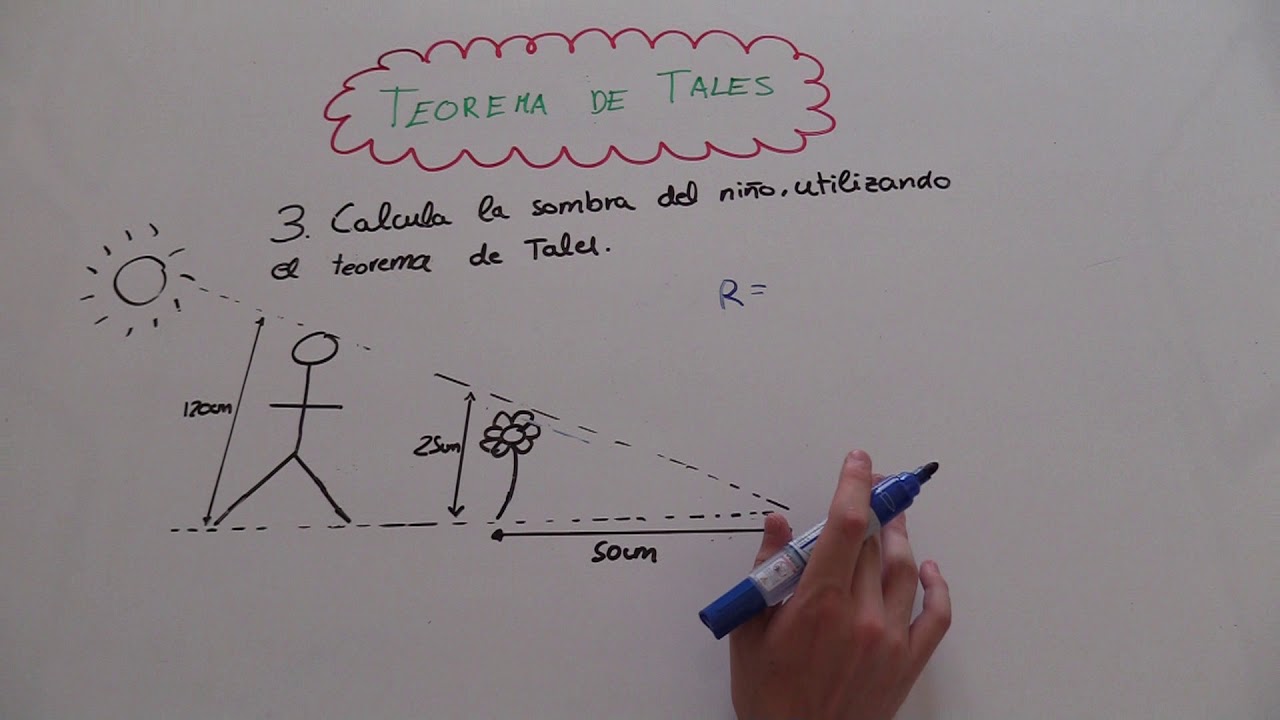
¿Qué es el Teorema de Tales?
El Teorema de Tales es un concepto fundamental en la geometría que establece una relación entre segmentos proporcionales en triángulos similares. Pero, ¿cómo se relaciona este teorema con nuestra vida diaria? A lo largo de este artículo exploraremos cómo este principio matemático encuentra aplicaciones prácticas en situaciones cotidianas.
El teorema en la arquitectura
Cuando observamos un edificio imponente, ¿alguna vez has pensado en cómo los arquitectos y diseñadores utilizan el Teorema de Tales en su trabajo? La proporcionalidad y la escala son elementos clave en la arquitectura, y este teorema les permite crear estructuras equilibradas y visualmente atractivas.
La importancia de las proporciones en el diseño arquitectónico
En el diseño de edificaciones, cada elemento debe guardar una proporción adecuada con respecto a los demás para lograr un resultado armónico. Desde la distribución de espacios hasta la altura de los techos, el Teorema de Tales guía a los arquitectos en la creación de espacios funcionales y estéticos.
Aplicaciones en la ingeniería civil
La ingeniería civil es otro campo donde el Teorema de Tales juega un papel crucial. Al diseñar puentes, carreteras y estructuras civiles, los ingenieros deben garantizar la estabilidad y la seguridad de las construcciones, y esto implica aplicar principios geométricos como los definidos por Tales de Mileto.
Garantizando la resistencia de las estructuras
Al calcular las cargas que soportarán los puentes, por ejemplo, los ingenieros deben tener en cuenta la proporcionalidad de los materiales utilizados. El Teorema de Tales les ayuda a determinar con precisión cómo distribuir el peso y diseñar estructuras capaces de resistir fuerzas externas.
En el mundo financiero: proporciones y rentabilidad
¿Sabías que el Teorema de Tales también se puede aplicar en el mundo de las finanzas? En la inversión, entender la relación entre el capital inicial, el rendimiento y el tiempo puede marcar la diferencia entre el éxito y el fracaso. La proporcionalidad es clave para maximizar la rentabilidad de una inversión.
Optimizando las inversiones
Al diversificar una cartera de inversión, es fundamental encontrar un equilibrio entre activos de alto y bajo riesgo. El Teorema de Tales nos recuerda que la proporcionalidad en la distribución de activos puede ayudar a minimizar las pérdidas y maximizar los beneficios a largo plazo.
El Teorema de Tales y la naturaleza
La naturaleza misma sigue patrones matemáticos sorprendentes, y el Teorema de Tales no es la excepción. Desde la disposición de las hojas en las ramas de un árbol hasta la estructura geométrica de los pétalos de una flor, la proporcionalidad definida por Tales se manifiesta en el entorno natural de manera fascinante.
Simetría y proporción en la biodiversidad
Los biólogos y ecologistas han observado cómo las proporciones matemáticas influyen en la simetría de los organismos vivos. La relación entre las partes de un ser vivo muchas veces sigue los principios geométricos que Tales postuló, revelando la armonía subyacente en la diversidad de la vida.
El Teorema de Tales en la tecnología
En un mundo cada vez más digital, la aplicación de conceptos matemáticos como el Teorema de Tales se extiende también al ámbito tecnológico. Desde el diseño de interfaces de usuario hasta la programación de algoritmos, la proporcionalidad y la relación entre elementos son fundamentales en la creación de tecnología intuitiva y eficiente.
Diseño de interfaces amigables
Cuando los diseñadores de software crean interfaces para aplicaciones y páginas web, buscan que la disposición de los elementos sea armoniosa y funcional. La proporcionalidad basada en principios como el Teorema de Tales les permite diseñar interfaces que facilitan la interacción del usuario y mejoran la experiencia de navegación.
¿Cómo aprender más sobre el Teorema de Tales y su importancia en la vida diaria?
Para profundizar en el conocimiento de este teorema y explorar su relevancia en diferentes áreas, te recomendamos investigar en libros de geometría, cursos en línea especializados y recursos educativos que aborden temas de matemáticas aplicadas. ¡Descubre cómo las proporciones matemáticas no solo son parte de fórmulas abstractas, sino también de nuestra cotidianidad!
Explorando la belleza de la geometría en nuestro entorno
El Teorema de Tales nos invita a reflexionar sobre la presencia de la proporcionalidad en nuestro entorno y cómo este principio geométrico ayuda a dar forma a nuestra realidad. ¿Te animas a identificar más ejemplos de su aplicación en tu vida diaria?
¿Qué otros campos además de la matemática aplican el Teorema de Tales?
El Teorema de Tales tiene aplicaciones en la arquitectura, la ingeniería civil, las finanzas, la biología y la tecnología, entre otros campos. Su relevancia trasciende las aulas de matemáticas.
¿Por qué es importante comprender la proporcionalidad en diversos contextos?
Entender la relación entre las magnitudes y dimensiones de diferentes elementos nos permite tomar decisiones informadas, resolver problemas de manera eficiente y apreciar la armonía presente en nuestro entorno.
¿Cómo puedo aplicar los conceptos del Teorema de Tales en mi vida diaria?
Observar la proporción y las relaciones entre objetos y situaciones cotidianas puede ayudarte a desarrollar un pensamiento crítico, mejorar tu capacidad de análisis y apreciar la belleza matemática que nos rodea.