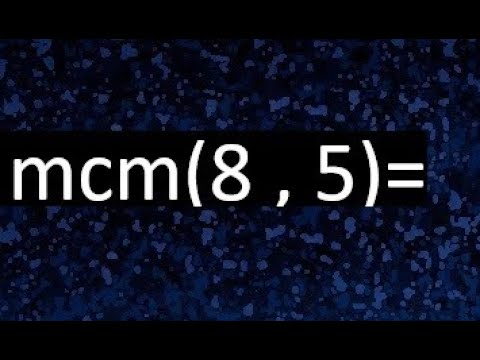En el mundo de las matemáticas, a menudo nos encontramos con situaciones en las que necesitamos encontrar el mínimo común múltiplo (MCM) de dos números. En este caso, nos enfrentamos al desafío de determinar el MCM de los números 8 y 5. ¿Te has preguntado cómo encontrar esta solución de manera efectiva?
Descifrando el concepto de Mínimo Común Múltiplo
El mínimo común múltiplo, también conocido como MCM, es el menor múltiplo común de dos o más números. En este caso, nos centraremos en los números 8 y 5. En términos simples, el MCM es el número más pequeño que es divisible por ambos números sin dejar residuo.
¿Por qué es importante comprender el MCM?
Entender el concepto de Mínimo Común Múltiplo es fundamental en diversas áreas de las matemáticas y la vida cotidiana. Desde problemas de fracciones hasta la programación computacional, el MCM juega un papel crucial en la resolución de problemas numéricos y en la optimización de procesos matemáticos.
La estrategia para hallar el MCM de 8 y 5
Para encontrar el Mínimo Común Múltiplo de 8 y 5, es importante seguir un enfoque sistemático. Una forma eficaz de abordar este problema es descomponer cada número en sus factores primos y luego identificar cuáles de estos factores se repiten y cuáles son únicos. Esta estrategia nos permitirá llegar al MCM deseado de manera precisa y rápida.
Factorización de 8 y 5
Empecemos por desglosar los números 8 y 5 en sus factores primos. El número 8 se descompone en 2 x 2 x 2, mientras que el número 5 es un número primo y no se puede factorizar más. Al analizar las descomposiciones de ambos números, podemos identificar los factores primos que los componen.
Identificación de los factores comunes y únicos
Ahora, analicemos los factores primos de 8 y 5 para determinar cuáles de ellos se repiten en ambas descomposiciones y cuáles son exclusivos de cada número. En este caso, el número 2 es el único factor común entre 8 y 5, mientras que 2 y 5 son factores únicos de cada número respectivamente.
El proceso de cálculo del MCM
Una vez identificados los factores comunes y únicos, el paso final consiste en multiplicar todos los factores comunes y únicos entre los números dados. En este caso, multiplicamos el factor común 2 una vez, el factor único 5 una vez y el factor único 2 tres veces para obtener el Mínimo Común Múltiplo de 8 y 5.
Calculando el MCM de 8 y 5
Al multiplicar los factores reconocidos, obtenemos el siguiente cálculo: 2 x 2 x 2 x 5 = 40. Por lo tanto, el Mínimo Común Múltiplo de 8 y 5 es 40. Esta solución nos proporciona el número más pequeño que es divisible por ambos 8 y 5 sin dejar residuos, cumpliendo así con la definición de MCM.
Aplicaciones prácticas del MCM
El concepto de Mínimo Común Múltiplo va más allá de la simple aritmética. En la programación informática, el MCM se utiliza en la optimización de algoritmos y la sincronización de procesos. En situaciones cotidianas, como la elaboración de calendarios o la planificación de entregas, el MCM juega un papel crucial en la organización eficiente de tareas y eventos.
Importancia del MCM en la vida diaria
Al comprender cómo encontrar el Mínimo Común Múltiplo de dos números, podemos aplicar este conocimiento a situaciones reales para simplificar tareas y resolver problemas de manera eficiente. Desde la distribución equitativa de recursos hasta la sincronización de actividades, el MCM nos brinda una herramienta matemática valiosa para enfrentar desafíos diversos.
Explorando más allá: conceptos relacionados con el MCM
Además de conocer cómo determinar el Mínimo Común Múltiplo de dos números específicos, es beneficioso familiarizarse con conceptos relacionados que amplíen nuestro entendimiento matemático. Entre estos conceptos se encuentran el máximo común divisor (MCD), las fracciones equivalentes y las propiedades generales de la aritmética.
El vínculo entre MCM y MCD
El Mínimo Común Múltiplo y el máximo común divisor están estrechamente relacionados en el ámbito de las matemáticas. Mientras que el MCM busca el menor múltiplo común entre dos o más números, el MCD busca el mayor divisor común. Ambos conceptos son fundamentales para simplificar fracciones y operaciones matemáticas más complejas.
Fracciones equivalentes y el MCM
Al comprender el Mínimo Común Múltiplo, podemos simplificar y comparar fracciones de manera efectiva. En situaciones donde necesitamos sumar o restar fracciones con diferentes denominadores, el MCM nos permite encontrar un denominador común para facilitar las operaciones. Esta habilidad es esencial en ámbitos como las finanzas, la ingeniería y la estadística.
¿Por qué es importante conocer el MCM en matemáticas?
El Mínimo Común Múltiplo es fundamental para simplificar operaciones numéricas, resolver problemas de proporcionalidad y optimizar procesos matemáticos en diversas áreas.
¿Cómo puedo aplicar el concepto de MCM en situaciones cotidianas?
El MCM se utiliza en la planificación de eventos, la organización de tareas recurrentes y la sincronización de actividades para mejorar la eficiencia y la productividad.
¿Cuál es la relación entre el MCM y el MCD?
El Mínimo Común Múltiplo busca el menor múltiplo común entre dos números, mientras que el máximo común divisor busca el mayor divisor común. Ambos conceptos son complementarios en el análisis matemático.
¿Cómo puedo practicar más ejercicios de MCM?
Existen numerosos recursos en línea, como aplicaciones y libros de ejercicios de matemáticas, que ofrecen una amplia gama de problemas para mejorar tu comprensión y habilidades en el cálculo del Mínimo Común Múltiplo.